Sources
LTI Omnidirectional Source
An LTI Omnidirectional Source is parameterized by taking the convolution between the transmitted signal and the impulse response from the source located at position, $\mathbf{p}_\mathrm{s}$.
We provide the geometry of the signal observation at position $\bm{\xi}$ due to the source, $\mathbf{p}_\mathrm{s}$ as follows
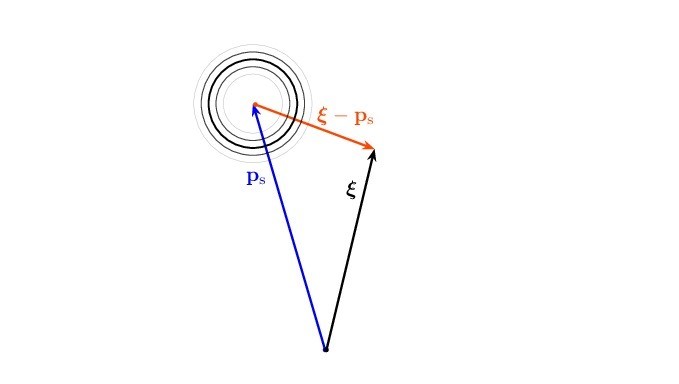
Mathematically, we define an LTI Omnidirectional Source as follows
\[\mathsf{q}(\bm{\xi},t)=\mathsf{p}(t) \overset{t}{*} \mathsf{h}(\bm{\xi},t;\,{\mathbf{p}_\mathrm{s}}).\]
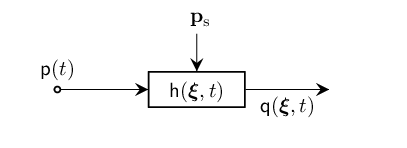
Defining an LTI Omnidirectional Source
We define an LTI Omnidirectional Source by calling LTIsourceO() with a transmitted signal, $\mathsf{p}(t)$ and the source position vector, $\mathbf{p}_\mathrm{s}$.
using LTVsystems
𝐩ₛ = [0.0, 0.0]
tₚ = 1.0e-06
p(t) = δn(t-tₚ,1.0e-07)
q = LTIsourceO(𝐩ₛ, p)LTI Omnidirectional SourceLTI Directional Source
An LTI Directional Source is parameterized by accounting the direction of the antenna which is defined by directional gain,
\[\mathrm{D}_\mathrm{s}\left(\bm{\xi};\,\textcolor{myLightSlateGrey} {\mathbf{p}_\mathrm{s},\bm{b}_\mathrm{s}}\right)= \mathrm{G}_\mathrm{s} \left(∠[\,\bm{b}\,,\,\bm{\xi}-\mathbf{p}_\mathrm{s}\,]\right)\]
where $∠[⋅,⋅]$ returns the angle between the two arguments and $\mathrm{G}_\mathrm{s}(\Theta)$ is the source antenna's $\textit{voltage gain}$ as a function of angle $\Theta$ relative to the beam center $\bm{b}_\mathrm{s}$.
Mathematically, an LTI Directional Source is given as follows
\[\mathsf{q}(\bm{\xi},t)=\mathsf{p}(t) \overset{t}{*} \mathsf{h}\big(\bm{\xi},t;\, \textcolor{myLightSlateGrey}{\mathbf{p}_\mathrm{s},\bm{b}_\mathrm{s},\mathrm{G}_\mathrm{s}(\cdot)}\big).\]
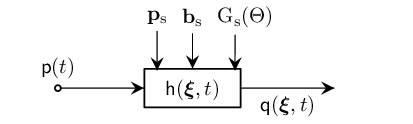
Defining an LTI Directional Source
We define an LTI Directional Source by calling LTIsourceDTI() with a source position, $\mathbf{p}_\mathrm{s}$, a transmitted signal, $\mathsf{p}(t)$, time-invariant beam center, $\bm{b}_\mathrm{s}$ and the source antenna's gain, $\mathrm{G}_\mathrm{s}(\Theta)$ as a function of angle $\Theta$ relative to the beam center $\bm{b}_\mathrm{s}$.
using LTVsystems
𝐩ₛ = [0.0, 0.0]
tₚ = 1.0e-06
p(t) = δn(t-tₚ,1.0e-07)
𝐛 = [1.0,0.0]
G(θ) = 𝒩ᵤ(θ, μ=0.0, σ=π/8)
q = LTIsourceDTI(𝐩ₛ, p, 𝐛, G)LTI Directional SourceStationary Directional Source with Time-Varying Beam Center
A Stationary Directional Source is parameterized by accounting the direction of the antenna with a time-varying (rotating) beam and is defined by directional gain as follows
\[\mathrm{D}_\mathrm{s}\left(\bm{\xi};\,\textcolor{myLightSlateGrey} {\mathbf{p}_\mathrm{s},\bm{b}_\mathrm{s}}\right)= \mathrm{G}_\mathrm{s} \left(∠[\,\bm{b}(t)\,,\,\bm{\xi}-\mathbf{p}_\mathrm{s}\,]\right),\]
where $∠[⋅,⋅]$ returns the angle between the two arguments and $\mathrm{G}_\mathrm{s}(\Theta)$ is the source antenna's $\textit{voltage gain}$ as a function of angle $\Theta$ relative to the beam center $\bm{b}_\mathrm{s}(t)$.
Mathematically, a Stationary Directional Source with time-varying beam center is given as follows
\[\mathsf{q}(\bm{\xi},t)=\mathsf{p}(t) \overset{t}{*} \mathsf{h}\big(\bm{\xi},t;\, \textcolor{myLightSlateGrey}{\mathbf{p}_\mathrm{s},\bm{b}_\mathrm{s}(\cdot),\mathrm{G}_\mathrm{s}(\cdot)}\big).\]
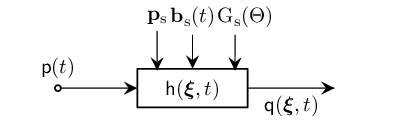
Defining an Stationary Directional Source with Time-Varying Beam Center
We define an Stationary Directional Source with time-varying beam center by calling STATsourceD() with a source position, $\mathbf{p}_\mathrm{s}$, a transmitted signal, $\mathsf{p}(t)$, a time-varying (rotating) beam center, $\bm{b}_\mathrm{s}(t)$ and the source antenna's gain, $\mathrm{G}_\mathrm{s}(\Theta)$ as a function of angle $\Theta$ relative to the beam center $\bm{b}_\mathrm{s}(t)$.
using LTVsystems
𝐩ₛ = [0.0, 0.0]
tₚ = 1.0e-06
p(t) = δn(t-tₚ,1.0e-07)
𝐛(t) = [cos(2π*10*t),0.0]/(norm(cos(2π*10*t)))
G(θ) = 𝒩ᵤ(θ, μ=0.0, σ=π/8)
q = STATsourceD(𝐩ₛ, p, 𝐛, G)Stationary Directional Source with Time-Varying Beam Center