Reflectors

Ideal Point Reflectors

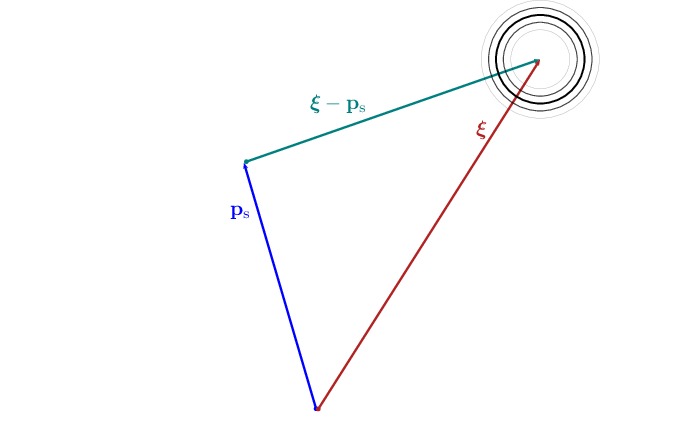
An ideal point reflector is parameterized by considering the reflection coefficients, $\mathsf{\alpha}_1,\mathsf{\alpha}_2,\ldots,\mathsf{\alpha}_n$ located at fixed positions, say $\bm{ξ}_1,\bm{ξ}_2,\ldots,\bm{ξ}_n$ as follows

\[\mathsf{f}(\bm{\xi}) = \sum_{n} \mathsf{\alpha}_n \delta(\bm{\xi} - \bm{\xi}_n).\]

Note that the reflection coefficients take negative values since we assume that the voltage is fixed at the reflector's end.

We provide the geometry of the reflection from the position $\bm{\xi}$ due to the source as follows

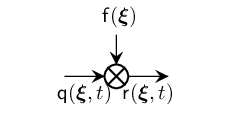
Mathematically, the reflection due to the LTI Omnidirectional Source is given by

\[\mathsf{r}(\bm{\xi},t) = \mathsf{f}(\bm{\xi}) \mathsf{q}(\bm{\xi},t).\]

Defining primary reflection due to ideal point reflector

We define the primary reflection due to the ideal point reflector by calling pointReflector() with reflection coefficient $\mathsf{\alpha}$ at position $\bm{\xi}$ and the source observation $\mathsf{q}(\xi,t)$ at position $\mathbf{p}_\mathrm{s}$.

using LTVsystems
𝐩ₛ =  [0.0, 0.0]
tₚ = 1.0e-06
p(t) = δn(t-tₚ,1.0e-07)
q = LTIsourceO(𝐩ₛ, p)
α = -0.7; 𝛏 = [3.75e-06c,0.0]
r = pointReflector(𝛏,α,q)

Primary Reflection

Continuous Reflectors as a Line Segment

We define a simple continuous reflector in term of a line segment, $AB$ of length, $L$ as follows

\[\mathsf{f}(\bm{\xi}) = \int_{0}^{L}\mathsf{\alpha}_0 \delta(\bm{\xi} - [\bm{\xi}_0+k\bm{u}]) \mathrm{d}k\]

where $\mathsf{\alpha}_0$ is a reflection coefficient, $\bm{ξ₀}$ is an initial position vector, $\bm{u}$ is an unit vector in the direction of $AB$ and $k$ is any scalar quantity.