Receivers

LTI Omnidirectional Receiver

In order to define LTI Omnidirectional Receiver, first we observed the signal due to the primary reflection.

We provide the geometry of the the signal observation at position, $\mathbf{p}_\mathrm{r}$ due to the primary reflection emitted from the position $\bm{\xi}$ as follows

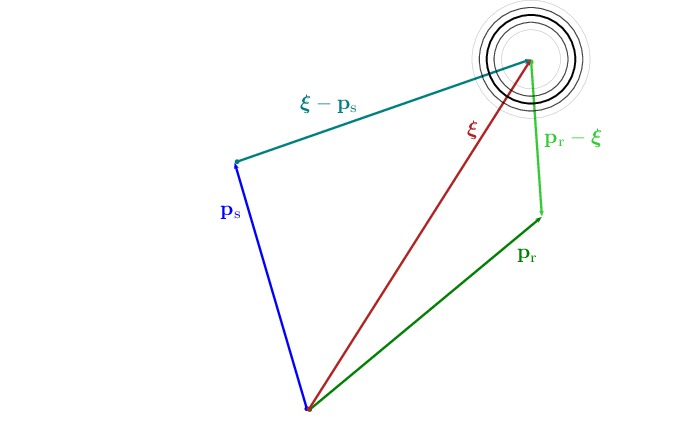
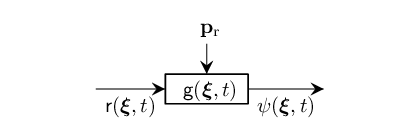
Mathematically, the signal observation at position, $\mathbf{p}_\mathrm{r}$ due to the primary reflection emitted from the position $\bm{\xi}$ is given by

\[\mathsf{\psi}(\bm{\xi},t) = \mathsf{r}(\bm{\xi},t) \overset{t}{*} \mathsf{g}\big(\bm{\xi},t;\,{\mathbf{p}_\mathrm{r}(\cdot)}\big).\]

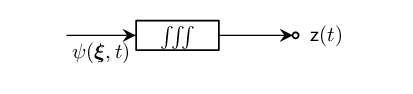
Finally, the signal observed by the receiver at position, $\mathbf{p}_\mathrm{r}$ due to the primary reflections is defined as follows

\[\mathsf{z}(t) = ∭_S \mathsf{\psi}(\bm{\xi},t) dS,\]

where $S$ is the entire spatial domain.

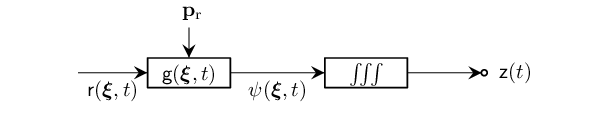
Defining an LTI Omnidirectional Receiver

First, we observed the reflected signal by calling pointReflector() then we define a LTI Omnidirectional Receiver by calling LTIreceiverO() with the reflected signal, $\mathsf{r}(\bm{\xi},t)$ and the receiver position, $\mathbf{p}_\mathrm{r}$.

using LTVsystems
𝐩ₛ =  [0.0, 0.0]
𝐩ᵣ =  𝐩ₛ
tₚ = 1.0e-06
p(t) = δn(t-tₚ,1.0e-07)
q = LTIsourceO(𝐩ₛ, p)
α = -0.7; 𝛏 = [3.75e-06c,0.0]
r = pointReflector(𝛏,α,q)
z = LTIreceiverO([r],𝐩ᵣ)

LTI Omnidirectional Receiver

LTI Directional Receiver

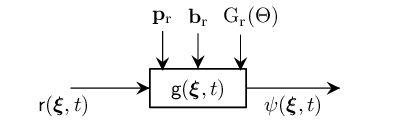
An LTI Directional Receiver is parameterized by accounting the direction of the antenna which is defined by directional gain,

\[\mathrm{D}_\mathrm{r}\left(\bm{\xi};\,\textcolor{myLightSlateGrey} {\mathbf{p}_\mathrm{r},\mathbf{b}_\mathrm{r}}\right)= \mathrm{G}_\mathrm{r} \left(∠[\,\mathbf{b}\,,\,\bm{\xi}-\mathbf{p}_\mathrm{r}\,]\right),\]

where $∠[⋅,⋅]$ returns the angle between the two arguments and $\mathrm{G}_\mathrm{r}(\Theta)$ is the receiver antenna's $\textit{voltage gain}$ as a function of angle $\Theta$ relative to the beam center $\mathbf{b}_\mathrm{r}$.

We define an LTI Directional Receiver by observing the signal due to the reflection given by taking convolution between the reflected signal, $\mathsf{r}(\bm{\xi},t)$ and the impulse response from the receiver located at position, $\mathbf{p}_\mathrm{r}$.

Mathematically, we can define the observed signal as follows

\[\mathsf{\psi}(\bm{\xi},t)=\mathsf{r}(\bm{\xi},t) \overset{t}{*} \mathsf{g}(\bm{\xi},t;\, \textcolor{myLightSlateGrey}{\mathbf{p}_\mathrm{r},\mathbf{b}_\mathrm{r}}).\]

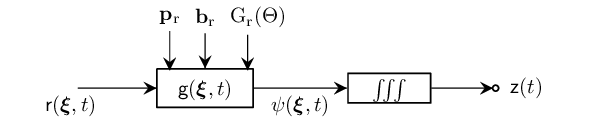
Finally, the signal, $\mathsf{z}(t)$ observed by the receiver at position $\mathbf{p}_\mathrm{r}$ due to the primary reflections is given by

\[\mathsf{z}(t) = ∭_S \mathsf{\psi}(\bm{\xi},t) dS,\]

where $S$ is the entire spatial domain.

Defining an LTI Directional Receiver

We define a LTI Directional Receiver by calling LTIreceiverDTI() with the defined reflected signal, $\mathsf{r}(\bm{\xi},t)$, time-invariant beam center, $\bm{b}_\mathrm{r}$ and the receiver antenna's gain, $\mathrm{G}_\mathrm{r}(\Theta)$ as a function of angle $\Theta$ relative to the beam center $\bm{b}_\mathrm{r}$.

using LTVsystems
𝐩ₛ =  [0.0, 0.0]
𝐩ᵣ =  𝐩ₛ
tₚ = 1.0e-06
p(t) = δn(t-tₚ,1.0e-07)
𝐛 = [1.0,0.0]
G(θ) = 𝒩ᵤ(θ, μ=0.0, σ=π/8)
q = LTIsourceDTI(𝐩ₛ, p, 𝐛, G)
α = -0.7; 𝛏 = [3.75e-06c,0.0]
r = pointReflector(𝛏,α,q)
z = LTIreceiverDTI([r],𝐩ᵣ,𝐛,G)

LTI Directional Receiver

Stationary Directional Receiver

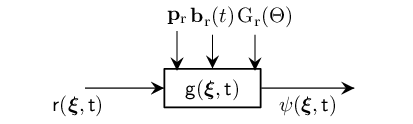
Stationary Directional Receiver with Time-Varying Beam Center

Mathematically, a Stationary Directional Receiver with time-varying (rotating) beam center is given as follows

\[\mathsf{\psi}(\bm{\xi},t)=\mathsf{r}(\bm{\xi},t) \overset{t}{*} \mathsf{g}(\bm{\xi},t;\, \textcolor{myLightSlateGrey}{\mathbf{p}_\mathrm{r},\mathbf{b}_\mathrm{r}(t)}).\]

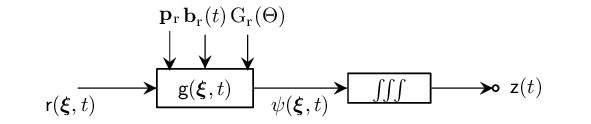
Finally, the signal, $\mathsf{z}(t)$ observed by the receiver at position $\mathbf{p}_\mathrm{r}$ due to the primary reflections is given by

\[\mathsf{z}(t) = ∭_S \mathsf{\psi}(\bm{\xi},t) dS,\]

where $S$ is the entire spatial domain.

Defining an Stationary Directional Receiver

We define a Stationary Directional Receiver by calling STATreceiverD() with the defined reflected signal, $\mathsf{r}(\bm{\xi},t)$, a time-varying (rotating) beam center, $\bm{b}_\mathrm{r}(t)$ and the receiver antenna's gain, $\mathrm{G}_\mathrm{r}(\Theta)$ as a function of angle $\Theta$ relative to the beam center $\bm{b}_\mathrm{r}(t)$.

using LTVsystems
𝐩ₛ =  [0.0, 0.0]
𝐩ᵣ =  𝐩ₛ
tₚ = 1.0e-06
p(t) = δn(t-tₚ,1.0e-07)
𝐛(t) = [cos(2π*10*t),0.0]/(norm(cos(2π*10*t)))
G(θ) = 𝒩ᵤ(θ, μ=0.0, σ=π/8)
q = STATsourceD(𝐩ₛ, p, 𝐛, G)
α = -0.7; 𝛏 = [3.75e-06c,0.0]
r = pointReflector(𝛏,α,q)
z = STATreceiverD([r],𝐩ᵣ,𝐛,G)

Stationary Directional Receiver with Time-Varying Beam Center