| Symbol | Type | Description |
|---|
| $t$ | scalar variable | time |
| $\bm{\xi}$ | vector variable | position |
| $\mathbf{p}_\mathrm{s}(t)$ | vector function of time | position of source |
| $\mathbf{p}_\mathrm{r}(t)$ | vector function of time | position of receiver |
| $\mathsf{h}_τ\big(\bm{\xi},t;\,{\mathbf{p}_\mathrm{s}(\cdot)}\big)$ | scalar function of position and time | LTI impulse response from $\mathbf{p}_\mathrm{s}(t)$ to $\bm{\xi}$ |
| $\mathsf{g}_τ\big(\bm{\xi},t;\,{\mathbf{p}_\mathrm{r}(\cdot)}\big)$ | scalar function of position and time | LTI impulse response from $\bm{\xi}$ to $\mathbf{p}_\mathrm{r}(t)$ |

- single omnidirectional source moving with a constant speed
- single omnidirectional receiver at same location as the source moving with a constant speed
- single stationary ideal point reflector
- the source emits an impulse
using LTVsystems
using Plots
s₁ = 0.30c
𝐯₁ = [1.0, 0.0]
tₚ = 1.0e-06
𝐩ₛ(t) = [-10.0e-06c,-1.5e-06c] .+ s₁.*𝐯₁.*(t-tₚ)
𝐩ᵣ(t) = 𝐩ₛ(t)
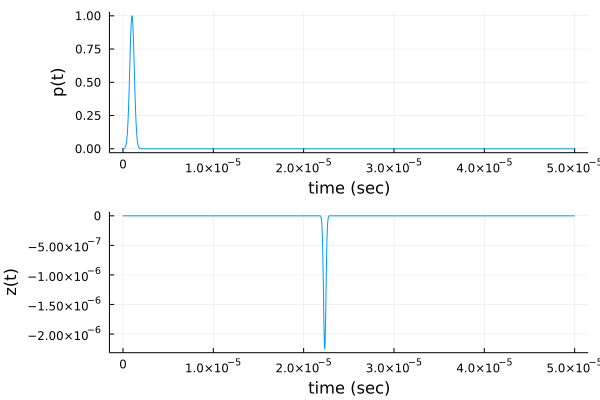
p(t) = δn(t-tₚ,2.5e-07)
q = LTVsourceO(𝐩ₛ, p)
α₀ = -0.7; 𝛏₀ = [3.75e-06c,0.0]
r = pointReflector(𝛏₀,α₀,q)
z = LTVreceiverO([r],𝐩ᵣ)
t=0.0:1.0e-08:50.0e-06
p1=plot(t,p, xlab="time (sec)", ylab="p(t)", legend=:false)
p2=plot(t,z(t), xlab="time (sec)", ylab="z(t)", legend=:false)
plot(p1,p2,layout=(2,1))