LTV Doppler Effect Modeling
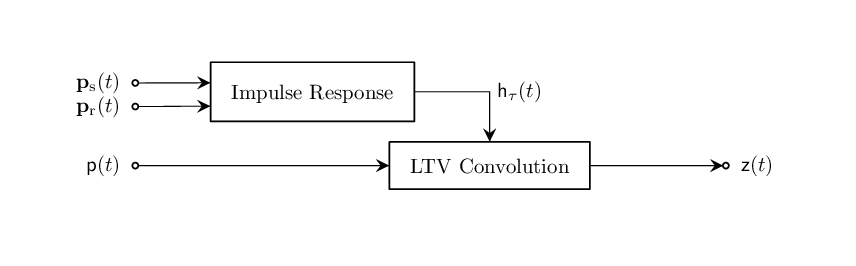
The LTV impulse response from an omnidirectional source located at position $\mathbf{p}_\mathrm{s}(t)$ to an omnidirectional receiver located at position $\mathbf{p}_\mathrm{r}(t)$ is given by
\[\mathsf{h}_\tau(t;\,{\mathbf{p}_\mathrm{s}(\cdot),\mathbf{p}_\mathrm{r}(\cdot)}) = \mathsf{A}(t_\mathrm{D}(\tau))\delta\big(t-\left[\tau + t_\mathrm{D}(\tau) \right]\big),\]
where $t_\mathrm{D}$ is the time-delay given as
\[t_\mathrm{D}(t) = \frac{\|\mathbf{p}_\mathrm{r}(t) - \mathbf{p}_\mathrm{s}(t) \|}{\mathrm{c}}\]
In order to observe the Doppler effect, we assume that the receiver is moving (with respect to the source) such as
\[\mathbf{p}_\mathrm{r}(t) = \mathbf{p}_\mathrm{s}(t) + \mathbf{p}_0 +\mathrm{s}\bm{v}t,\]
\[\|\mathbf{p}_\mathrm{r}(t)-\mathbf{p}_\mathrm{s}(t)\| = \|\mathbf{p}_0 + \mathrm{s}\bm{v}t\|.\]
The observation of the source at the position $\mathbf{p}_\mathrm{r}(t)$ is given by
\[\mathsf{z}(t) = \mathsf{A}\left(\frac{\mathrm{s}\frac{\mathrm{c}t \pm (\mathbf{p}_0 \cdot \bm{v})}{\mathrm{c} \mp \mathrm{s}}}{\mathrm{c}}\right)\mathsf{p}\left(\frac{\mathrm{c}t \pm (\mathbf{p}_0 \cdot \bm{v})}{\mathrm{c} \mp \mathrm{s}}\right).\]
Scenario A [Sinusoidal signal, moving transmitter and stationary receiver]
Scenario Assumptions
- single omnidirectional source moving with a constant speed
- single stationary omnidirectional receiver
- the source emits a sinusoidal signal
Doppler Modeling in Time Domain
For scenario A, we provide the position of the moving source $\mathbf{p}_\mathrm{s}(t)$, the receiver position at $\mathbf{p}_\mathrm{r}.$
The received signal at $\mathbf{p}_\mathrm{r}$ will be delayed in time given by
\[t_\mathrm{D}(t) = \frac{\|\mathbf{p}_\mathrm{r} - \mathbf{p}_\mathrm{s}(t) \|}{\mathrm{c}}\]
In order to observe the Doppler effect, we assume that the source is moving with a constant velocity (with respect to the receiver) and the receiver is stationary such as
\[\mathbf{p}_\mathrm{r} = \mathbf{p}_\mathrm{s}(t)+ \mathbf{p}_0+\mathrm{s}\bm{v}t,\]
\[\mathbf{p}_\mathrm{r} - \mathbf{p}_\mathrm{s}(t) = \mathbf{p}_0+\mathrm{s}\bm{v}t,\]
\[\|\mathbf{p}_\mathrm{r} - \mathbf{p}_\mathrm{s}(t)\| = \|\mathbf{p}_0+\mathrm{s}\bm{v}t\|,\]
where $\|\bm{v}\|=1.$
Consider the source emits a sinusoidal signal given by
\[\mathsf{p}(t) = \cos(\omega (t-t_\mathrm{p})),\]
where $\omega$ is the frequency in radian per second.
We observe the signal at the position $\mathbf{p}_\mathrm{r}$ is given by
\[\mathsf{z}(t) = \mathsf{A}\left(\frac{\mathrm{s}(\mathrm{c}t \pm (\mathbf{p}_0 \cdot \bm{v}))}{\mathrm{c}(\mathrm{c} \mp \mathrm{s})}\right)\mathsf{\cos}\left(\frac{\mathrm{c}\omega(t-t_\mathrm{p}) \pm (\mathbf{p}_0 \cdot \bm{v}) }{\mathrm{c} \mp \mathrm{s} }\right).\]
using LTVsystems
using Plots
s = 0.45c
𝐯 = [1.0, 0.0]
𝐩ₛ₀= [-15.0e-06c,0.0]
𝐩ᵣ = [2.0e-06c,1.5e-06c]
f = 5e05
ω = 2π*f
tₚ = 1.0e-06
𝐩ₛ(t) = 𝐩ₛ₀ .+ s.*𝐯.*(t-tₚ)
p(t) = 10cos(ω*(t-tₚ))
q = LTVsourceO(𝐩ₛ, p)
z = LTIreceiverO([q],𝐩ᵣ)
t=0.0:1.0e-08:150.0e-06
p1=plot(t,p, xlab="time (sec)", ylab="p(t)", legend=:false)
p2=plot(t,z(t), xlab="time (sec)", ylab="z(t)", legend=:false)
plot(p1,p2,layout=(2,1),size=(800,800))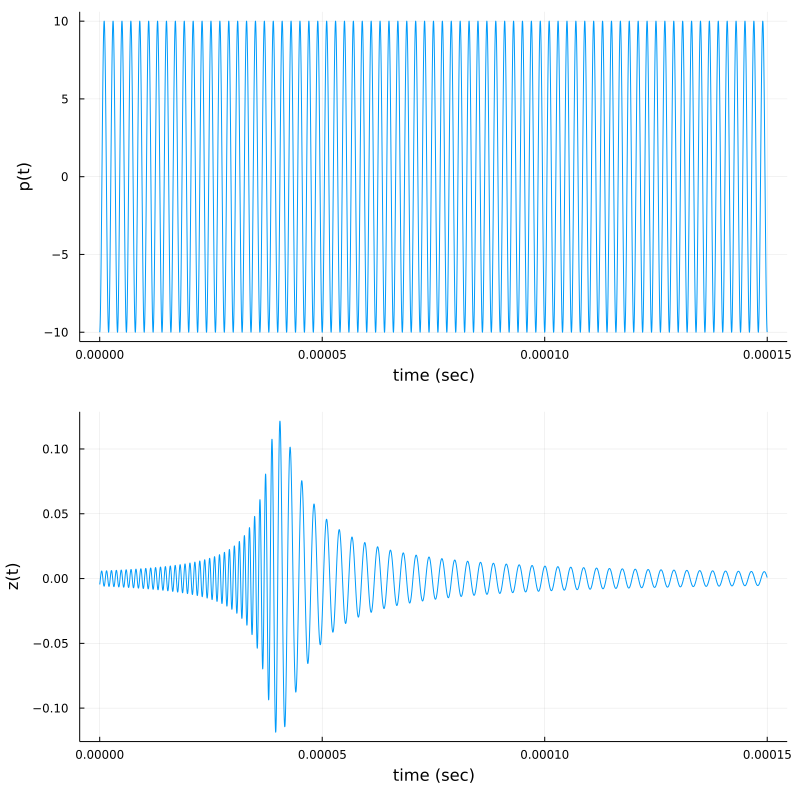
Scenario B [Sinusoidal signal, stationary transmitter and moving receiver]
Scenario Assumptions
- single stationary omnidirectional source
- single omnidirectional receiver moving with a constant speed
- the source emits a sinusoidal signal
Doppler Modeling in Time Domain
For scenario B, we provide the position of the stationary source $\mathbf{p}_\mathrm{s}$, the moving receiver position $\mathbf{p}_\mathrm{r}(t).$
The received signal at $\mathbf{p}_\mathrm{r}(t)$ will be delayed in time given by
\[t_\mathrm{D}(t) = \frac{\|\mathbf{p}_\mathrm{r}(t) - \mathbf{p}_\mathrm{s} \|}{\mathrm{c}}\]
In order to observe the Doppler effect, we assume that the receiver is moving with a constant velocity (with respect to the source) and the source is stationary such as
\[\mathbf{p}_\mathrm{s} = \mathbf{p}_\mathrm{r}(t)+ \mathbf{p}_0+\mathrm{s}\bm{v}t,\]
\[\mathbf{p}_\mathrm{s} - \mathbf{p}_\mathrm{r}(t) = \mathbf{p}_0+\mathrm{s}\bm{v}t,\]
\[\|\mathbf{p}_\mathrm{s} - \mathbf{p}_\mathrm{r}(t)\| = \|\mathbf{p}_0+\mathrm{s}\bm{v}t\|,\]
where $\|\bm{v}\|=1.$
Consider the source emits a sinusoidal signal given by
\[\mathsf{p}(t) = \cos(\omega (t-t_\mathrm{p})),\]
where $\omega$ is the frequency in radian per second.
using LTVsystems
using Plots
𝐩ₛ = [-15.0e-06c,-1.5e-06c]
s = 0.45c
𝐯 = [-1.0, 0.0]
tₚ = 1.0e-06
𝐩ᵣ₀ = [10.0e-06c,0.0]
f = 5e05
𝐩ᵣ(t) = 𝐩ᵣ₀ .+ s.*𝐯.*(t-tₚ)
p(t) = 10cos(2π*f*(t-tₚ))
q = LTIsourceO(𝐩ₛ, p)
z = LTVreceiverO([q],𝐩ᵣ)
t=0.0:1.0e-08:150.0e-06
p1=plot(t,p, xlab="time (sec)", ylab="p(t)", legend=:false)
p2=plot(t,z(t), xlab="time (sec)", ylab="z(t)", legend=:false)
plot(p1,p2,layout=(2,1),size=(800,800))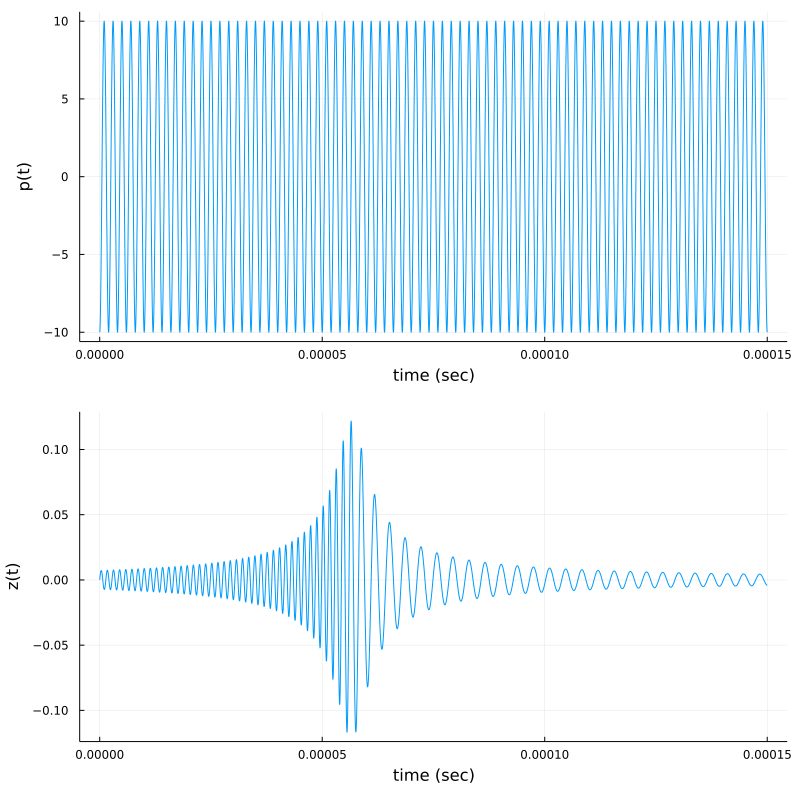
Scenario C [Sinusoidal signal, transmitter and receiver moving towards each other with a constant speed]
Scenario Assumptions
- single omnidirectional source moving with a constant speed
- single omnidirectional receiver moving with a constant speed
- the source emits a sinusoidal signal
using LTVsystems
using Plots
s₁ = 0.50c
𝐯₁ = [1.0, 0.0]
s₂ = 0.25c
𝐯₂ = [1.0, 0.0]
tₚ = 1.0e-06
f = 5e05
𝐩ₛ(t) = [-10.0e-06c,-1.5e-06c] .+ s₁.*𝐯₁.*(t-tₚ)
𝐩ᵣ(t) = [5.0e-06c,0.0] .+ s₂.*𝐯₂.*(t-tₚ)
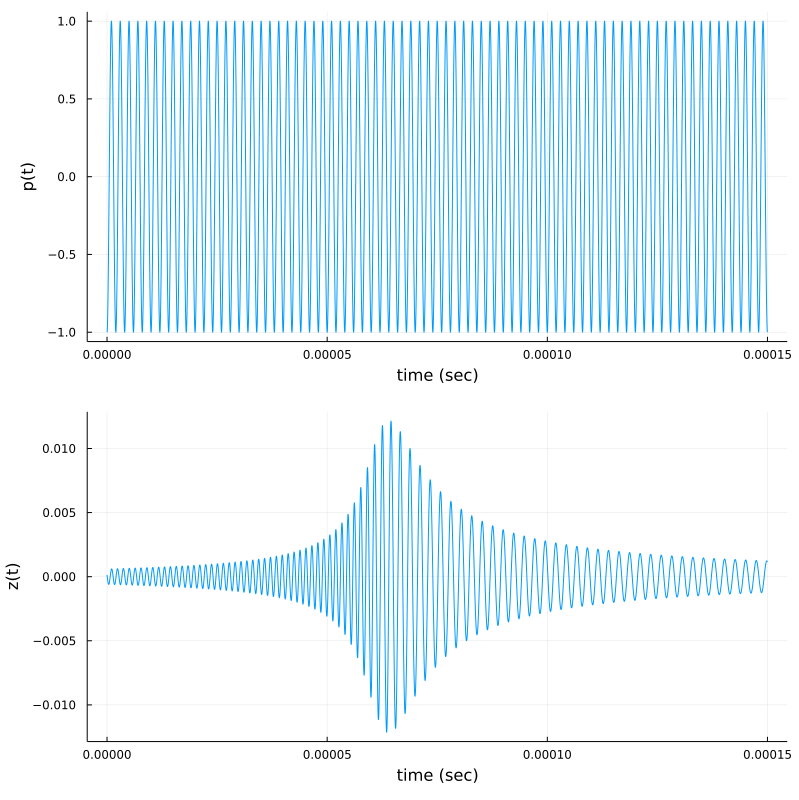
p(t) = cos(2π*f*(t-tₚ))
q = LTVsourceO(𝐩ₛ, p)
z = LTVreceiverO([q],𝐩ᵣ)
t=0.0:1.0e-08:150.0e-06
p1=plot(t,p, xlab="time (sec)", ylab="p(t)", legend=:false)
p2=plot(t,z(t), xlab="time (sec)", ylab="z(t)", legend=:false)
plot(p1,p2,layout=(2,1),size=(800,800))