LTI Directional Modeling
| Symbol | Type | Description |
|---|---|---|
| $\mathbf{b}_\mathrm{s}$ | vector | source beam center |
| $\mathbf{b}_\mathrm{r}$ | vector | receiver beam center |
| $\Theta$ | scalar | angle relative to beam center |
| $\angle(\bm{u},\bm{v})$ | operator | returns the angle between two vectors |
| $\mathrm{G}_\mathrm{s}(\Theta)$ | scalar function of angle | Gain of the source antenna |
| $\mathrm{G}_\mathrm{r}(\Theta)$ | scalar function of angle | Gain of the receiver antenna |
| $\mathrm{D}_\mathrm{s}\big(\bm{\xi};\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s}}\big)$ | scalar function of position | directivity of source |
| $\mathsf{h}\big(\bm{\xi},t;\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s},\mathrm{G}_\mathrm{s}(\cdot)}\big)$ | scalar function of position and time | LTI impulse response from $\mathbf{p}_\mathrm{s}$ to $\bm{\xi}$ |
| $\mathrm{D}_\mathrm{r}\big(\bm{\xi};\,{\mathbf{p}_\mathrm{r},\mathbf{b}_\mathrm{r}}\big)$ | scalar function of position | directivity of receiver |
| $\mathsf{g}\big(\bm{\xi},t;\,{\mathbf{p}_\mathrm{r},\mathbf{b}_\mathrm{r},\mathrm{G}_\mathrm{r}(\cdot)}\big)$ | scalar function of position and time | LTI impulse response from $\bm{\xi}$ to $\mathbf{p}_\mathrm{r}$ |

The LTI impulse response from $\mathbf{p}_\mathrm{s}$ to $\bm{\xi}$ is given by
\[\mathsf{h}(\bm{\xi},t;\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s},\mathrm{G}_\mathrm{s}(\cdot)}) = \mathrm{D}_\mathrm{s}\left(\bm{\xi};\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s}}\right) \mathsf{A}\left(\frac{\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|} {\mathrm{c}}\right) \delta\left(t-\frac{\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|}{\mathrm{c}}\right),\]
where $\mathrm{D}_\mathrm{s}\left(\bm{\xi};\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s}}\right)$ is the directional gain defined by
\[\mathrm{D}_\mathrm{s}\left(\bm{\xi};\,\textcolor{myLightSlateGrey} {\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s}}\right)= \mathrm{G}_\mathrm{s} \left(∠[\,\mathbf{b}\,,\,\bm{\xi}-\mathbf{p}_\mathrm{s}\,]\right).\]
The signal observed at position $\bm{\xi}$ and time $t$ due to the source emitting from position $\mathbf{p}_\mathrm{s}$ is given as
\[\begin{aligned} \mathsf{q}(\bm{\xi},t) &= \mathsf{p}(t) \overset{t}{*} \mathsf{h}(\bm{\xi},t;\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s},\mathrm{G}_\mathrm{s}(\cdot)}) \\ &=\mathrm{D}_\mathrm{s}\left(\bm{\xi};\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s}}\right) \mathsf{A}\left(\frac{\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|} {\mathrm{c}}\right) \mathsf{p}\left(t-\frac{\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|}{\mathrm{c}}\right). \end{aligned}\]
The reflection due to source is given by
\[\mathsf{r}(\bm{\xi},t) = \mathsf{f}(\bm{\xi}) \mathsf{q}(\bm{\xi},t).\]
The LTI impulse response from an arbitrary position $\bm{\xi}$ to the receiver at position $\mathbf{p}_\mathrm{r}$ is given by
\[\mathsf{g}(\bm{\xi},t;\,{\mathbf{p}_\mathrm{r},\mathbf{b}_\mathrm{r},\mathrm{G}_\mathrm{r}(\cdot)}) = \mathrm{D}_\mathrm{r}\left(\bm{\xi};\,{\mathbf{p}_\mathrm{r},\mathbf{b}_\mathrm{r}}\right) \mathsf{A}\left(\frac{\|\mathbf{p}_\mathrm{r}-\bm{\xi}\|}{\mathrm{c}}\right) \delta\left(t-\frac{\|\mathbf{p}_\mathrm{r}-\bm{\xi}\|}{\mathrm{c}}\right).\]
where $\mathrm{D}_\mathrm{r}\left(\bm{\xi};\,{\mathbf{p}_\mathrm{r},\mathbf{b}_\mathrm{r}}\right)$ is the directional gain defined by
\[\mathrm{D}_\mathrm{r}\left(\bm{\xi};\,\textcolor{myLightSlateGrey} {\mathbf{p}_\mathrm{r},\mathbf{b}_\mathrm{r}}\right)= \mathrm{G}_\mathrm{r} \left(∠[\,\mathbf{b}\,,\,\bm{\xi}-\mathbf{p}_\mathrm{r}\,]\right).\]
The signal observed at $\mathbf{p}_\mathrm{r}$ due to the reflection from the position $\bm{\xi}$ is given by
\[\begin{aligned} \mathsf{\psi}(\bm{\xi},t) &= \mathsf{r}(\bm{\xi},t) \overset{t}{*} \mathsf{g}\big(\bm{\xi},t;\,{\mathbf{p}_\mathrm{r},\mathbf{b}_\mathrm{r},\mathrm{G}_\mathrm{r}(\cdot)}\big) \\ &= \mathrm{D}_\mathrm{r}\left(\bm{\xi};\,{\mathbf{p}_\mathrm{r},\mathbf{b}_\mathrm{r}}\right) \mathsf{A}\left(\frac{\|\mathbf{p}_\mathrm{r}-\bm{\xi}\|}{\mathrm{c}}\right) \mathsf{r}\left(\bm{\xi},t-\frac{\|\mathbf{p}_\mathrm{r}-\bm{\xi}\|}{\mathrm{c}}\right). \end{aligned}\]
Scenario A [Single pulse, single reflector, transmitter and receiver at same location with single beam direction]
Scenario Assumptions
- single stationary directional source
- single stationary receiver at same location as the source
- two stationary ideal point reflectors
- the source emits a pulse
Given the assumptions, we simulate the following geometry for scenario A.
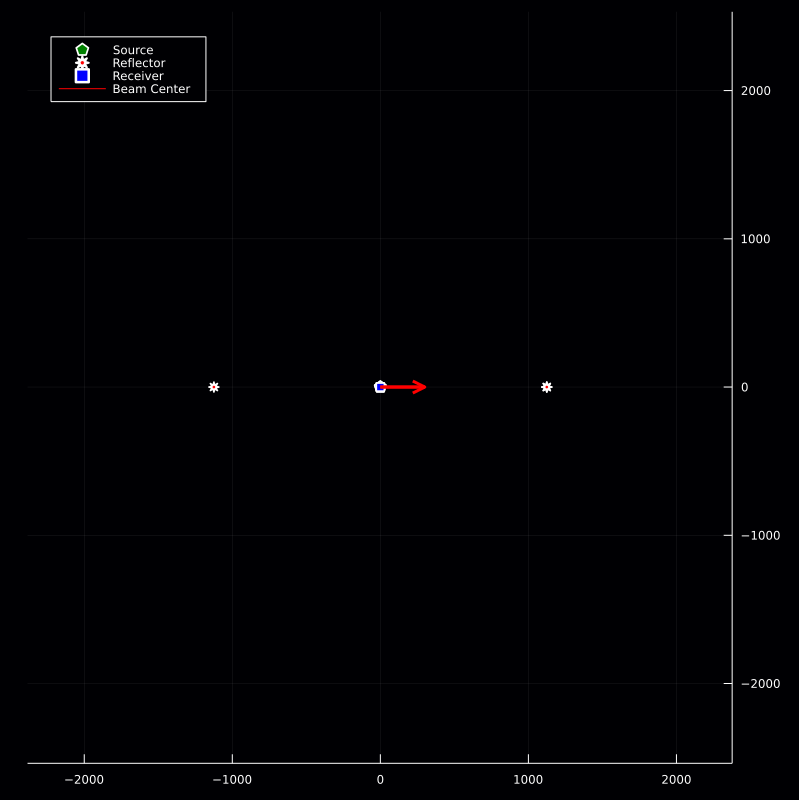
Forward Modeling
For scenario A, we provided the position of the directional source $𝐩ₛ$, the directional receiver's position $𝐩ᵣ$, being at the same location $(𝐩ₛ=𝐩ᵣ)$, the transmitted signal $\mathsf{p}(t)$, and an ideal point reflector $\bm{\xi}_0$.
Now the expression for the reflector function is given by
\[\mathsf{f}(\bm{\xi}) = \mathsf{\alpha}_0 \delta(\bm{\xi} - \bm{\xi}_0).\]
We compute the reflection due to the directional source as follows
\[\mathsf{r}(\bm{\xi},t) = \mathsf{\alpha}_0 \delta(\bm{\xi} - \bm{\xi}_0) \mathrm{D}_\mathrm{s}\left(\bm{\xi};\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s}}\right) \mathsf{A}\left(\frac{\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|} {\mathrm{c}}\right) \mathsf{p}\left(t-\frac{\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|}{\mathrm{c}}\right).\]
Finally, the closed form expression of the observed signal, $\mathsf{z}(t)$ with $(𝐩ₛ=𝐩ᵣ)$ is given by
\[\mathsf{z}(t) = \mathsf{\alpha}_0 \mathrm{D}_ \mathrm{s}\left(\bm{\xi}_0;\,{\mathbf{p}_\mathrm{s}, \mathbf{b}_\mathrm{s}}\right)\mathsf{A}^2 \left(\frac{\|\mathbf{p}_\mathrm{s}-\bm{\xi}_0\|} {\mathrm{c}}\right)\mathsf{p}\left(t -2\frac{\|\mathbf{p}_\mathrm{s}-\bm{\xi}_0\|}{\mathrm{c}}\right).\]
using LTVsystems
using Plots
𝐩ₛ = [0.0, 0.0]
𝐩ᵣ = 𝐩ₛ
tₚ = 1.0e-06
p(t) = δn(t-tₚ,1.0e-07)
𝐛 = [1.0,0.0]
G(θ) = 𝒩ᵤ(θ, μ=0.0, σ=π/64)
q = LTIsourceDTI(𝐩ₛ,p,𝐛,G)
α₀ = -0.7; 𝛏₀ = [3.75e-06c,0.0]
α₁ = -0.7; 𝛏₁ = [-3.75e-06c,0.0]
r = pointReflector([𝛏₀,𝛏₁],[α₀,α₁],[q])
z = LTIreceiverO(r,𝐩ᵣ)
t=0.0:1.0e-08:25.0e-06
p1 = plot(t,p, xlab="time (sec)", ylab="p(t)", legend=:false)
p2 = plot( t, z(t), xlab="time (sec)", ylab="z(t)", legend=:false)
plot(p1,p2,layout=(2,1),size=(800,800))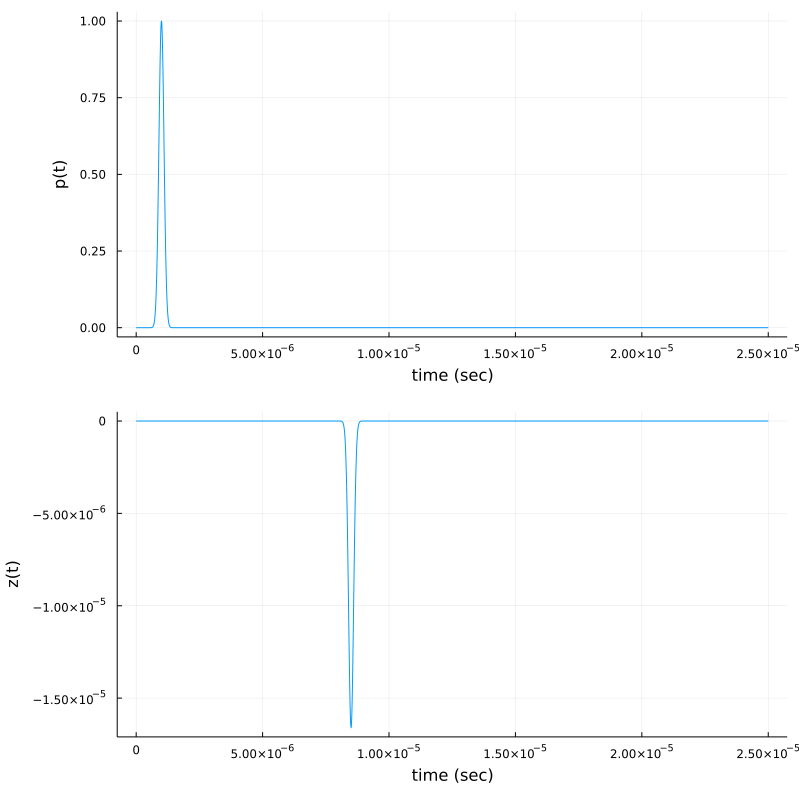
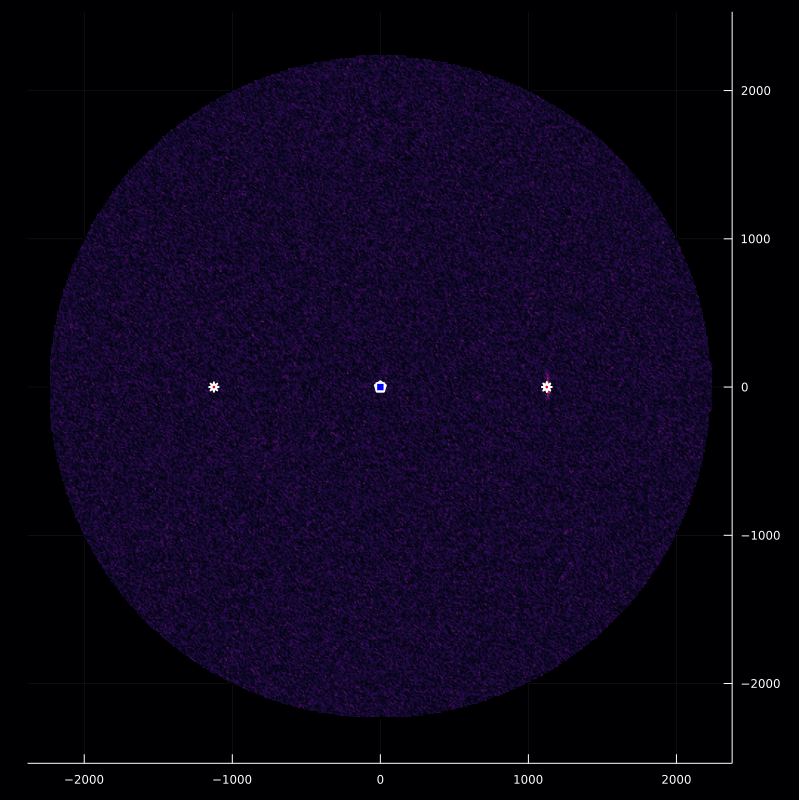
Inverse Modeling
Given the scenario A assumptions, we obtained the received signal, $\mathsf{z}(t)$. Now by considering the transmitted signal as a pulse given by
\[\mathsf{p}(t)=δ(t-t_\mathrm{p})\]
we estimate the reflector function as follows
\[\hat{\mathsf{f}}(\bm{\xi}) = \dfrac{\mathsf{z}\left(t_\mathrm{p}+\frac{2\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|}{\mathrm{c}}\right)\mathrm{D}_\mathrm{s}\left(\bm{\xi};\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s}}\right)} {\mathsf{A}^2\big(\frac{\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|}{\mathrm{c}}\big) } .\]
using LTVsystems
using Plots
𝐩ₛ = [0.0, 0.0]
𝐩ᵣ = 𝐩ₛ
tₚ = 1.0e-06
p(t) = δn(t-tₚ,1.0e-07)
𝐛 = [1.0,0.0]
G(θ) = 𝒩ᵤ(θ, μ=0.0, σ=π/64)
q = LTIsourceDTI(𝐩ₛ,p,𝐛,G)
α₀ = -0.7; 𝛏₀ = [3.75e-06c,0.0]
α₁ = -0.7; 𝛏₁ = [-3.75e-06c,0.0]
r = pointReflector([𝛏₀,𝛏₁],[α₀,α₁],[q])
z = LTIreceiverO(r,𝐩ᵣ)
D(ξ::Vector{Float64}) = G(angleBetween(𝐛, ξ.-𝐩ₛ))
f(ξ::Vector{Float64}) = (z(tₚ+ 2(norm(ξ-𝐩ₛ))/c).*D(ξ::Vector{Float64}))/(A(norm(ξ-𝐩ₛ)/c))^2
inversePlot2D([q],r,[z],f) 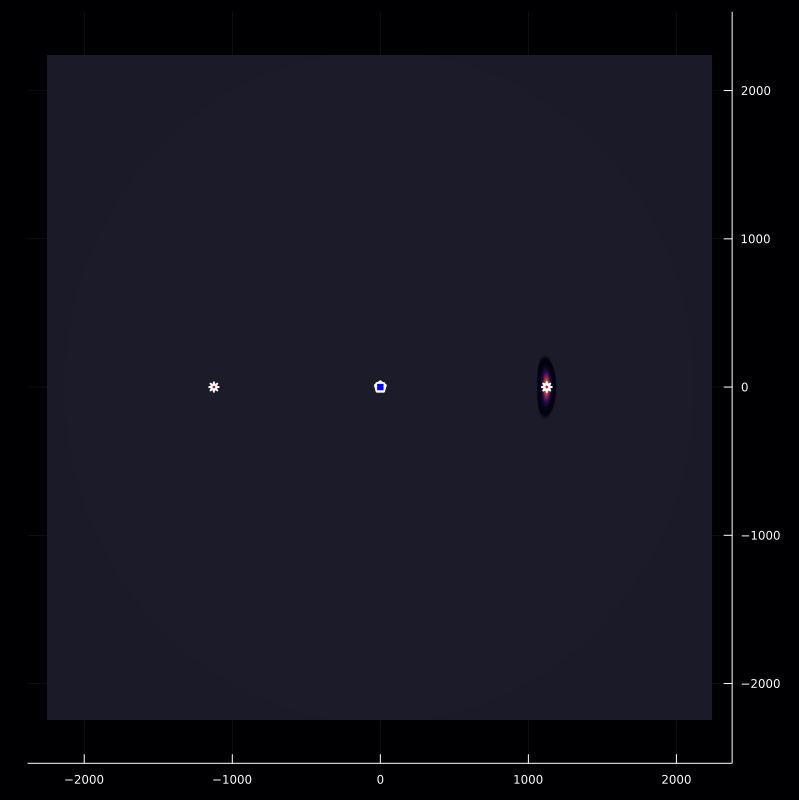
Scenario B [Single pulse, single reflector, transmitter and receiver at different location with single beam direction]
Scenario Assumptions
- single stationary directional source
- single stationary receiver
- two stationary ideal point reflectors
- the source emits a pulse
Given the assumptions, we simulate the following geometry for scenario B.
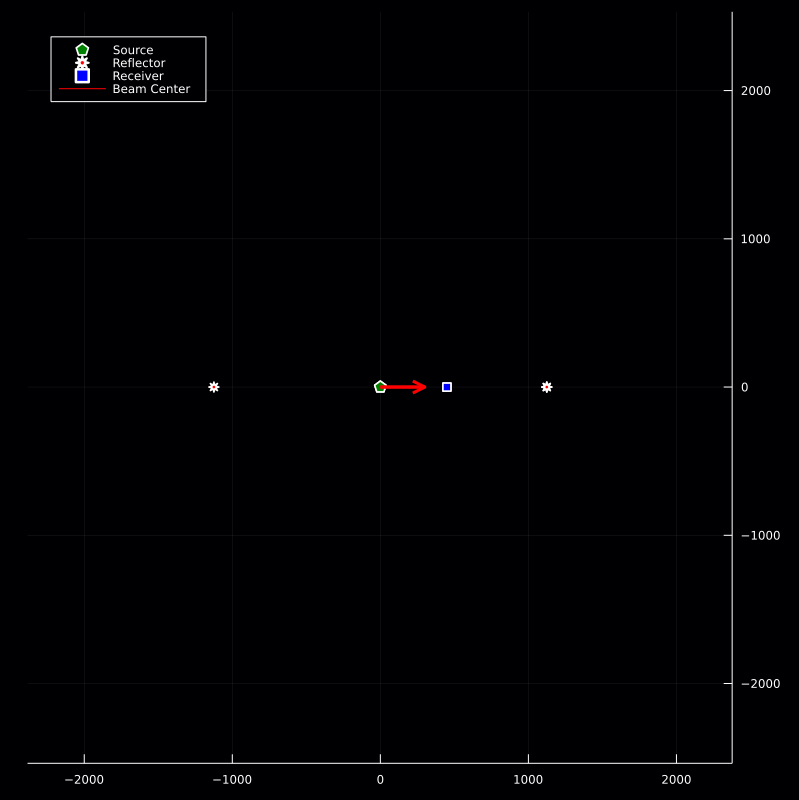
Forward Modeling
For scenario B, we provided the position of the directional source $𝐩ₛ$, the directional receiver's position $𝐩ᵣ$, the transmitted signal $\mathsf{p}(t)$, and an ideal point reflector $\bm{\xi}_0$.
Now the expression for the reflector function is given by
\[\mathsf{f}(\bm{\xi}) = \mathsf{\alpha}_0 \delta(\bm{\xi} - \bm{\xi}_0).\]
We compute the reflection due to the directional source as follows
\[\mathsf{r}(\bm{\xi},t) = \mathsf{\alpha}_0 \delta(\bm{\xi} - \bm{\xi}_0) \mathrm{D}_\mathrm{s}\left(\bm{\xi};\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s}}\right) \mathsf{A}\left(\frac{\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|} {\mathrm{c}}\right) \mathsf{p}\left(t-\frac{\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|}{\mathrm{c}}\right).\]
Finally, the closed form expression of the observed signal, $\mathsf{z}(t)$ is given by
\[\mathsf{z}(t) = \mathsf{\alpha}_0 \mathrm{D}_\mathrm{s}\left(\bm{\xi}_0;\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s}}\right) \mathsf{A}\left(\frac{\|\mathbf{p}_\mathrm{r}-\bm{\xi}_0\|}{\mathrm{c}}\right) \mathsf{A}\left(\frac{\|\bm{\xi}_0- \mathbf{p}_\mathrm{s}\|}{\mathrm{c}}\right) \mathsf{p}\left(t- \frac{\|\mathbf{p}_\mathrm{r}-\bm{\xi}_0\|+\|\bm{\xi}_0- \mathbf{p}_\mathrm{s}\|}{\mathrm{c}}\right).\]
using LTVsystems
using Plots
𝐩ₛ = [0.0, 0.0]
𝐩ᵣ = [1.5e-06c, 0.0]
tₚ = 1.0e-06
p(t) = δn(t-tₚ,1.0e-07)
𝐛 = [1.0,0.0]
G(θ) = 𝒩ᵤ(θ, μ=0.0, σ=π/64)
q = LTIsourceDTI(𝐩ₛ,p,𝐛,G)
α₀ = -0.7; 𝛏₀ = [3.75e-06c,0.0]
α₁ = -0.7; 𝛏₁ = [-3.75e-06c,0.0]
r = pointReflector([𝛏₀,𝛏₁],[α₀,α₁],[q])
z = LTIreceiverO(r,𝐩ᵣ)
t=0.0:1.0e-08:25.0e-06
p1 = plot(t,p, xlab="time (sec)", ylab="p(t)", legend=:false)
p2 = plot( t, z(t), xlab="time (sec)", ylab="z(t)", legend=:false)
plot(p1,p2,layout=(2,1),size=(800,800))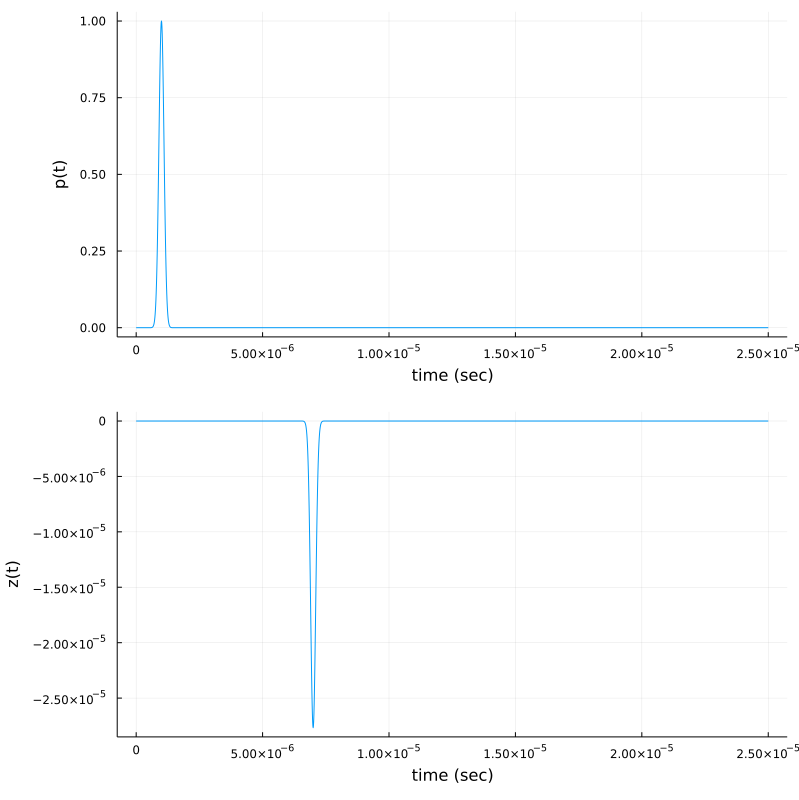
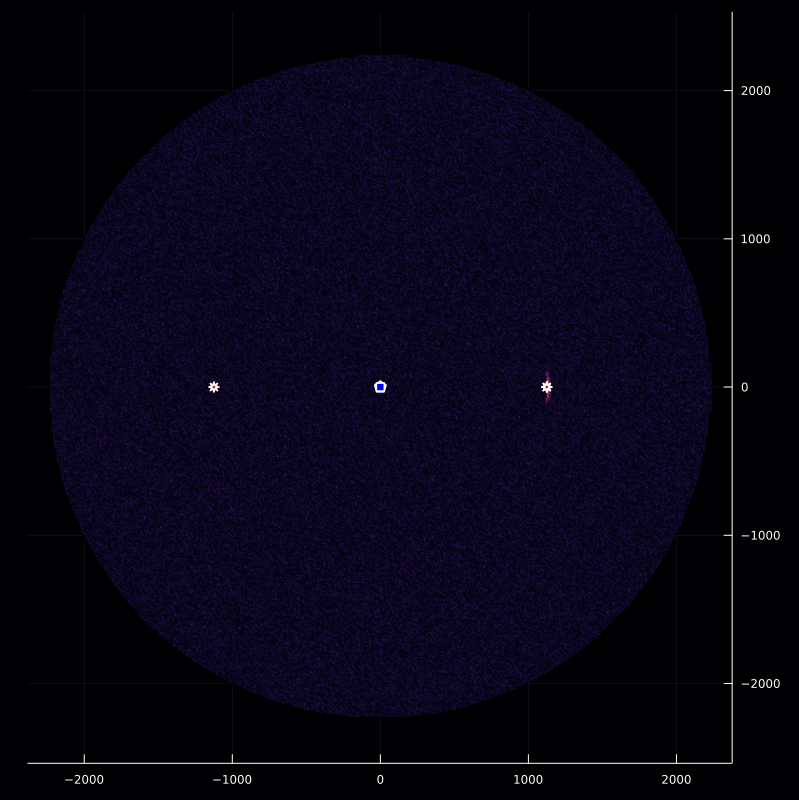
Inverse Modeling
Given the scenario B assumptions, we obtained the received signal, $\mathsf{z}(t)$. Now by considering the transmitted signal as a pulse given by
\[\mathsf{p}(t)=δ(t-t_\mathrm{p})\]
we estimate the reflector function as follows
\[\hat{\mathsf{f}}(\bm{\xi}) = \dfrac{\mathsf{z}\left(t_\mathrm{p}+\frac{\|\mathbf{p}_\mathrm{r}- \bm{\xi}\|+\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|} {\mathrm{c}} \right)\mathrm{D}_\mathrm{s}\left(\bm{\xi};\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s}}\right)}{\mathsf{A}\big(\frac{\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|}{\mathrm{c}}\big) \mathsf{A}\big(\frac{\|\mathbf{p}_\mathrm{r}-\bm{\xi}\|}{\mathrm{c}}\big)} .\]
using LTVsystems
using Plots
𝐩ₛ = [0.0, 0.0]
𝐩ᵣ = [1.5e-06c, 0.0]
tₚ = 1.0e-06
p(t) = δn(t-tₚ,1.0e-07)
𝐛 = [1.0,0.0]
G(θ) = 𝒩ᵤ(θ, μ=0.0, σ=π/64)
q = LTIsourceDTI(𝐩ₛ,p,𝐛,G)
α₀ = -0.7; 𝛏₀ = [3.75e-06c,0.0]
α₁ = -0.7; 𝛏₁ = [-3.75e-06c,0.0]
r = pointReflector([𝛏₀,𝛏₁],[α₀,α₁],[q])
z = LTIreceiverO(r,𝐩ᵣ)
Dₛ(ξ::Vector{Float64}) = G(angleBetween(𝐛, ξ.-𝐩ₛ))
f(ξ::Vector{Float64}) = (z(tₚ+(norm(ξ-𝐩ₛ) .+ norm(𝐩ᵣ-ξ))./c).*Dₛ(ξ::Vector{Float64}))/(A(norm(ξ-𝐩ₛ)/c).*A(norm(𝐩ᵣ-ξ)/c))
inversePlot2D([q],r,[z],f)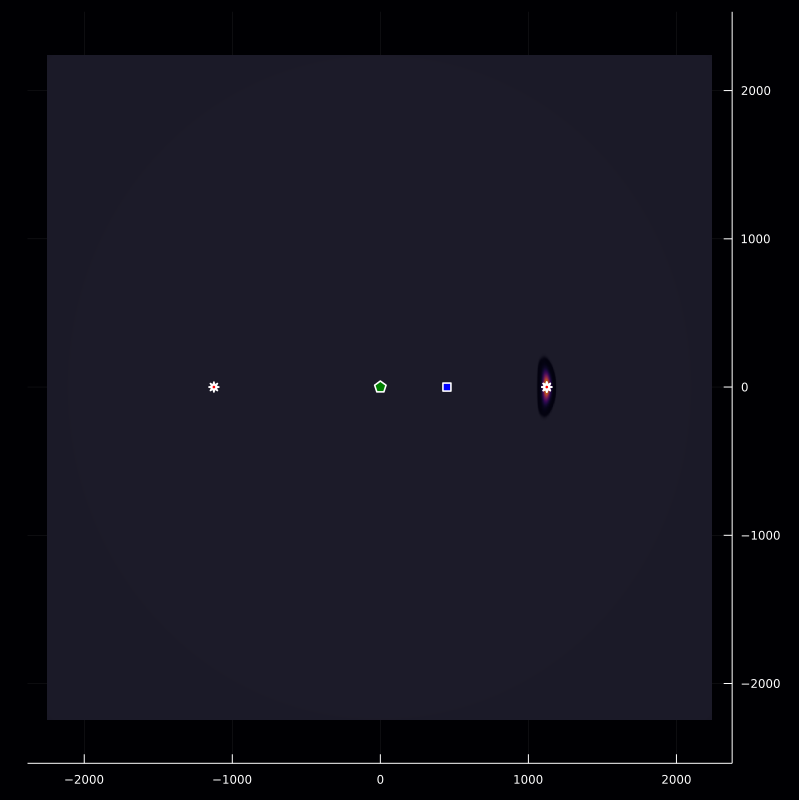
Scenario C [Pulse train, single reflector, transmitter and receiver at same location with single beam direction and random white noise]
Scenario Assumptions
- single stationary directional source
- single stationary directional receiver at the same location as source
- single ideal point reflector
- the source emits pulse train with single beam
- random white noise
Given the assumptions, we simulate the following geometry for scenario C.
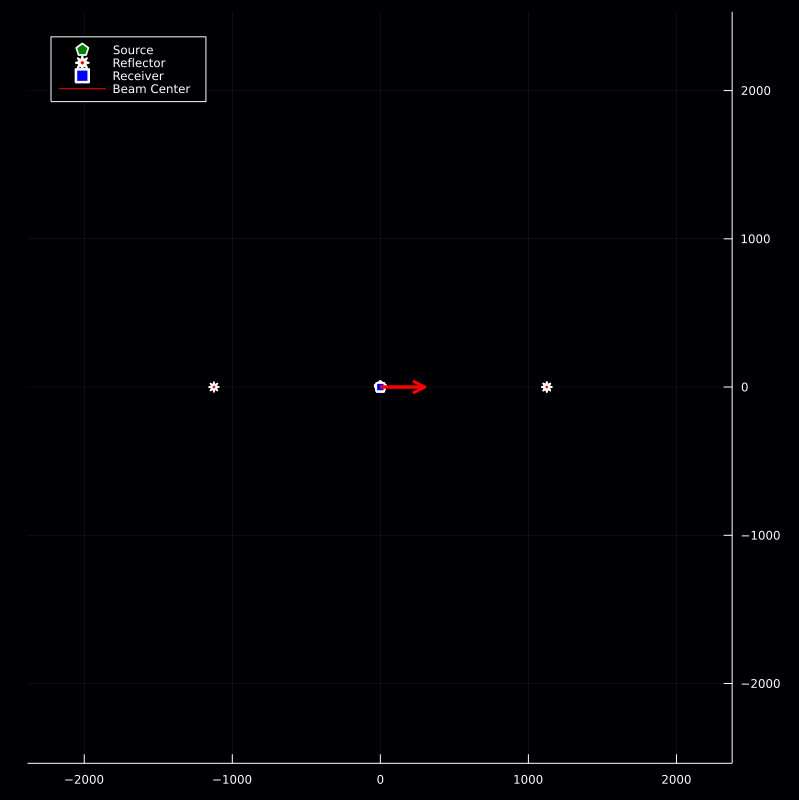
Forward Modeling
For scenario C, we provided the position of the directional source $𝐩ₛ$, the directional receiver's position $𝐩ᵣ$, being at the same location $(𝐩ₛ=𝐩ᵣ)$, the transmitted signal $\mathsf{p}(t)$, and an ideal point reflector $\bm{\xi}_0$.
Now the expression for the reflector function is given by
\[\mathsf{f}(\bm{\xi}) = \mathsf{\alpha}_0 \delta(\bm{\xi} - \bm{\xi}_0).\]
We compute the reflection due to the directional source as follows
\[\mathsf{r}(\bm{\xi},t) = \mathsf{\alpha}_0 \delta(\bm{\xi} - \bm{\xi}_0) \mathrm{D}_\mathrm{s}\left(\bm{\xi};\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s}}\right) \mathsf{A}\left(\frac{\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|} {\mathrm{c}}\right) \mathsf{p}\left(t-\frac{\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|}{\mathrm{c}}\right).\]
Finally, the closed form expression of the observed signal, $\mathsf{z}(t)$ with $(𝐩ₛ=𝐩ᵣ)$ is given by
\[\mathsf{z}(t) = \mathsf{\alpha}_0 \mathrm{D}_ \mathrm{s}\left(\bm{\xi}_0;\,{\mathbf{p}_\mathrm{s}, \mathbf{b}_\mathrm{s}}\right)\mathsf{A}^2 \left(\frac{\|\mathbf{p}_\mathrm{s}-\bm{\xi}_0\|} {\mathrm{c}}\right)\mathsf{p}\left(t -2\frac{\|\mathbf{p}_\mathrm{s}-\bm{\xi}_0\|}{\mathrm{c}}\right).\]
using LTVsystems
using Plots
𝐩ₛ = [0.0, 0.0]
𝐩ᵣ = [0.0, 0.0]
T = 15.0e-6
tₚ = 1.0e-06
p(t) = δn(mod(t-tₚ,T),1.0e-7)
𝐛 = [1.0,0.0]
G(θ) = 𝒩ᵤ(θ, μ=0.0, σ=π/48)
q = LTIsourceDTI(𝐩ₛ,p,𝐛,G)
α₀ = -0.7; 𝛏₀ = [3.75e-06c,0.0]
α₁ = -0.7; 𝛏₁ = [-3.75e-06c,0.0]
r = pointReflector([𝛏₀,𝛏₁],[α₀,α₁],[q])
z = LTIreceiverO(r,𝐩ᵣ)
t=0.0:T/100:5T
p1 = plot(t,p, xlab="time (sec)", ylab="p(t)", legend=:false)
p2 = plot( t, z(t), xlab="time (sec)", ylab="z(t)", legend=:false)
plot(p1,p2,layout=(2,1),size=(800,800))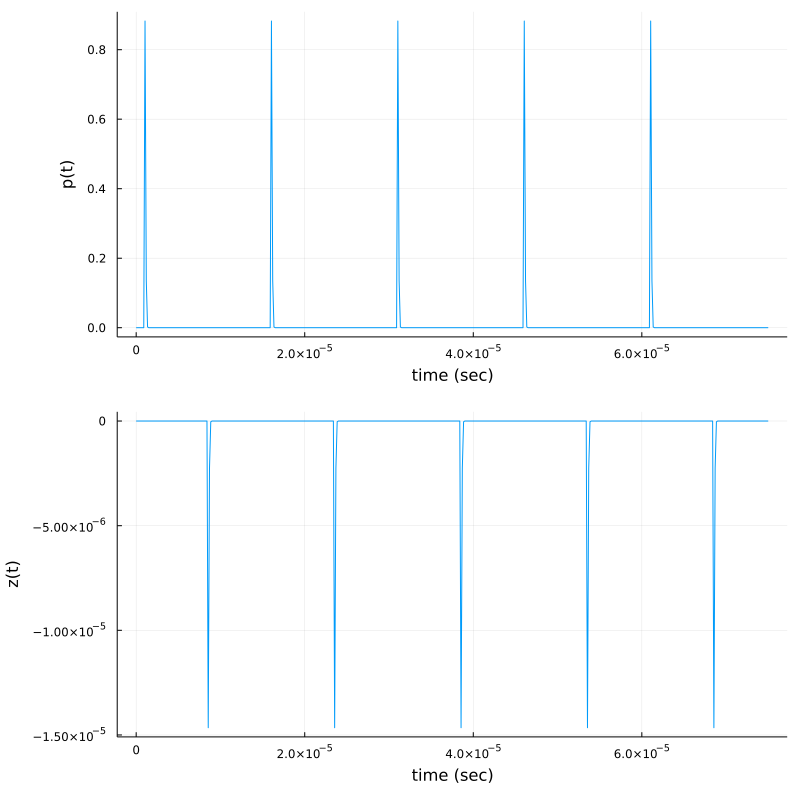
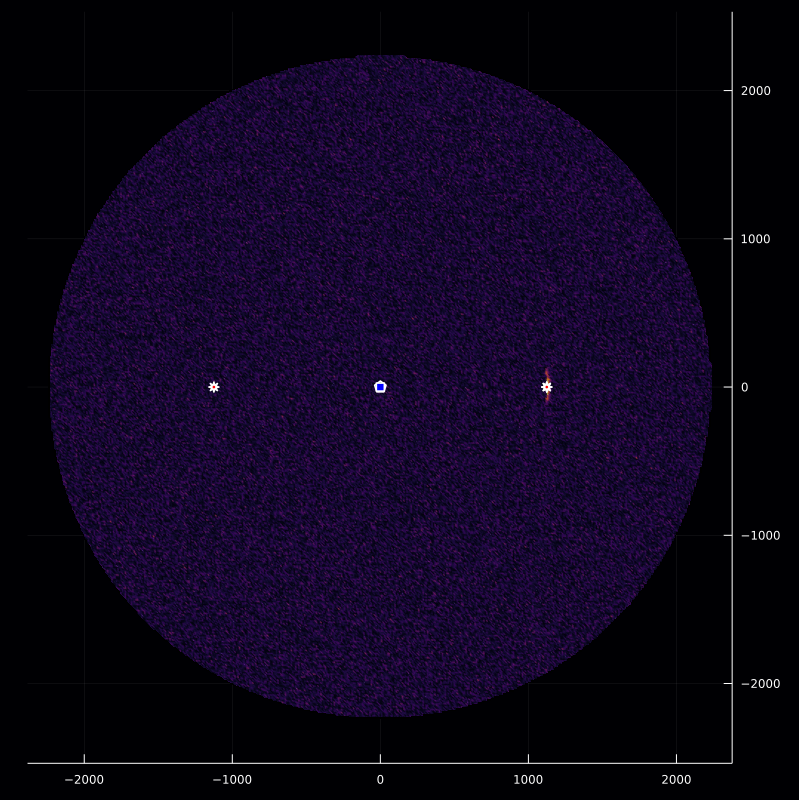
Inverse Modeling
Given the scenario C assumptions, we obtained the received signal, $\mathsf{z}(t)$. Now by considering the transmitted signal as a pulse train given by
\[\mathsf{p}(t)=δ(\mathrm{mod}(t-t_\mathrm{p},\mathrm{T})),\]
we compute the reflector function, $\mathsf{f}_k$ with respect to the pulse train, $k\mathrm{T}$ where $k \in \mathbf{Z}$ and $\mathrm{T}$ is the pulse repetition rate, along with the random white noise as follows
\[\mathsf{f}_k(\bm{\xi})=\dfrac{\mathsf{z}\left(t_\mathrm{p}+k\mathrm{T}+\frac{2\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|}{\mathrm{c}}\right)\mathrm{D}_\mathrm{s}\left(\bm{\xi};\,{\mathbf{p}_\mathrm{s},\mathbf{b}_\mathrm{s}}\right)} {\mathsf{A}^2\big(\frac{\|\bm{\xi}-\mathbf{p}_\mathrm{s}\|}{\mathrm{c}}\big)}.\]
Finally, the reflector function is given as follows
\[\hat{\mathsf{f}}(\bm{\xi}) = \frac{∑_{k=0}^{M-1} \mathsf{f}_k(\bm{\xi})}{M},\]
where $M$ is the number of pulses.
using LTVsystems
using Plots
𝐩ₛ = [0.0, 0.0]
𝐩ᵣ = [0.0, 0.0]
T = 15.0e-6
tₚ = 1.0e-06
p(t) = δn(mod(t-tₚ,T),1.0e-7)
𝐛 = [1.0,0.0]
G(θ) = 𝒩ᵤ(θ, μ=0.0, σ=π/48)
q = LTIsourceDTI(𝐩ₛ,p,𝐛,G)
α₀ = -0.7; 𝛏₀ = [3.75e-06c,0.0]
α₁ = -0.7; 𝛏₁ = [-3.75e-06c,0.0]
r = pointReflector([𝛏₀,𝛏₁],[α₀,α₁],[q])
z = LTIreceiverO(r,𝐩ᵣ)
Dₛ(ξ::Vector{Float64}) = G(angleBetween(𝐛, ξ.-𝐩ₛ))
f₁(ξ::Vector{Float64})=ifelse(norm(ξ)>c*T/2, NaN, (0.75e-01randn(1)[1]+ z(tₚ+0*T+(2norm(ξ-𝐩ₛ))./c).*Dₛ(ξ)./(A(norm(ξ-𝐩ₛ)/c))^2))
f₂(ξ::Vector{Float64})=ifelse(norm(ξ)>c*T/2, NaN, (0.75e-01randn(1)[1]+z(tₚ+1*T+(2norm(ξ-𝐩ₛ))./c).*(Dₛ(ξ))^2 ./(A(norm(ξ-𝐩ₛ)/c))^2))
f₃(ξ::Vector{Float64})=ifelse(norm(ξ)>c*T/2, NaN, (0.75e-01randn(1)[1]+ z(tₚ+2*T+(2norm(ξ-𝐩ₛ))./c).*(Dₛ(ξ))^2 ./(A(norm(ξ-𝐩ₛ)/c))^2))
f₄(ξ::Vector{Float64})=ifelse(norm(ξ)>c*T/2, NaN, (0.75e-01randn(1)[1]+ z(tₚ+3*T+(2norm(ξ-𝐩ₛ))./c).*(Dₛ(ξ))^2 ./(A(norm(ξ-𝐩ₛ)/c))^2))
f₅(ξ::Vector{Float64})=ifelse(norm(ξ)>c*T/2, NaN, (0.75e-01randn(1)[1]+ z(tₚ+4*T+(2norm(ξ-𝐩ₛ))./c).*(Dₛ(ξ))^2 ./(A(norm(ξ-𝐩ₛ)/c))^2))
f(ξ::Vector{Float64}) = (f₁(ξ).+f₂(ξ).+f₃(ξ).+f₄(ξ).+f₅(ξ))/5
p11=inversePlot2D([q],r,[z],f₁)
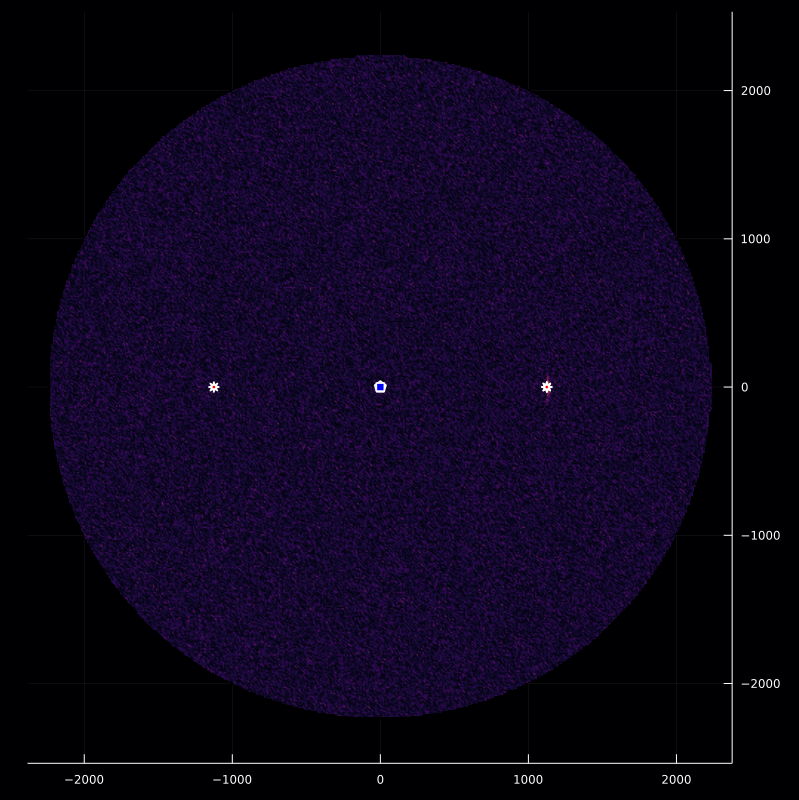
p12=inversePlot2D([q],r,[z],f₂)
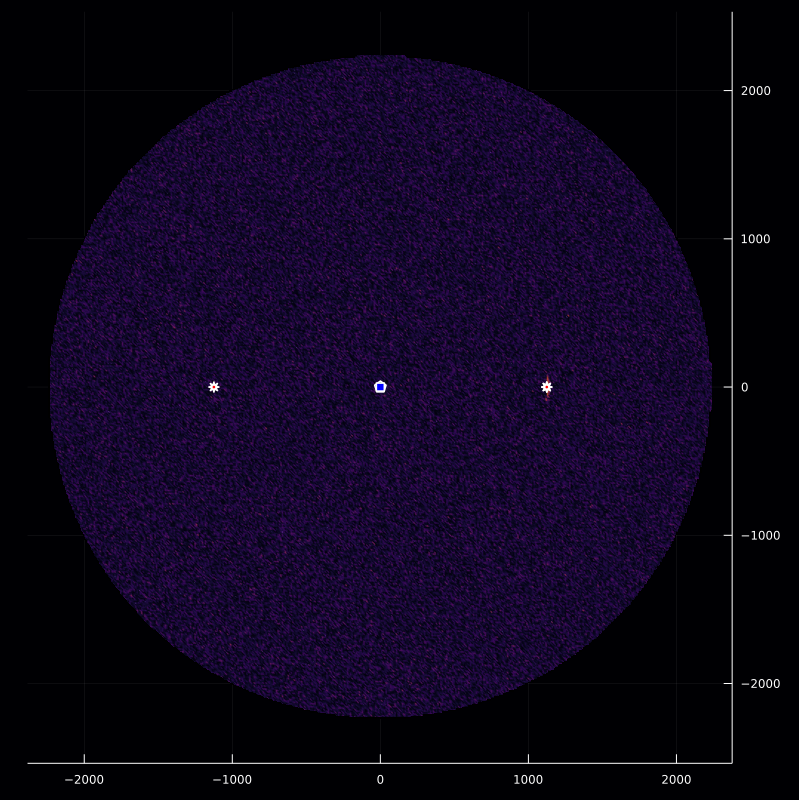
p13=inversePlot2D([q],r,[z],f₃)
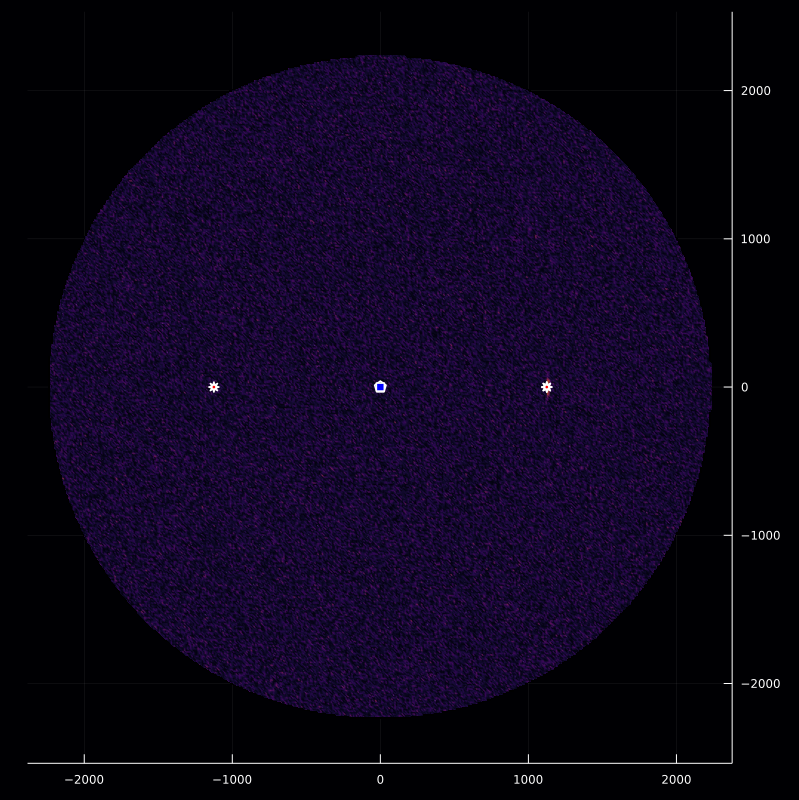
p14=inversePlot2D([q],r,[z],f₄)
p15=inversePlot2D([q],r,[z],f₅)
p6=inversePlot2D([q],r,[z],f)