Edit on GitHub

Basic Signal Models

Fourier Series

Consider a component set consisting of a set of harmonically related SHCs

S≜{⋯ ,C−1,C0,C1,⋯ }, Ck={ak,kω0,ϕk00}, k=0,±1,±2,…,±∞.\mathscr{S}\triangleq\left\{\cdots,\mathscr{C}_{-1},\mathscr{C}_0,\mathscr{C}_1,\cdots\right\},~\mathscr{C}_k = \left\{a_k,k\omega_0, \phi_k\vphantom{0^0}\right\},~k = 0,\pm 1,\pm 2,\ldots,\pm\infty .

As a result, the components are of the form

ψk(t;Ck00)=ake j(kω0t+ϕk)\psi_k \left(t ; \mathscr{C}_k \vphantom{0^0}\right) = a_k \mathrm{e}^{\,\mathrm{j}(k\omega_0 t +\phi_k)}

and the AM–FM model corresponding to this set is a Fourier Series

z(t)=∑k=−∞∞ake j(kω0t+ϕk).z(t) = \sum\limits_{k=-\infty}^{\infty} a_k \mathrm{e}^{\,\mathrm{j}(k\omega_0 t +\phi_k)}.

Partial Sums of Fourier Series

The AM–FM model corresponding to a partial sum (over kk) of a Fourier series

z(t)=∑k=−KKake j(kω0t+ϕk)z(t) = \sum\limits_{k=-K}^{K} a_k \mathrm{e}^{\,\mathrm{j}(k\omega_0 t +\phi_k)}

can be visualized. Additionally, the 3D IS corresponding to partial sum (over kk)

S(t,ω,s;S)=2π∑k=−KKψk(t;Ck00)  ⁣2δ ⁣(ω−ωk,s−sk(t)00)\mathcal{S}(t,\omega,s;\mathscr{S}) = 2 \pi \sum\limits_{k=-K}^{K} \psi_k\left( t ; \mathscr{C}_k \vphantom{0^0}\right) \,\!{}^{2}\delta\!\left(\omega-\omega_k,s-s_k(t)\vphantom{0^0}\right)

and the 2D IS corresponding to partial sum (over kk) (i.e. time-frequency plane)

S(t,ω;S)=2π∑k=−KKψk(t;Ck00)  ⁣δ ⁣(00ω−ωk00)\mathcal{S}(t,\omega;\mathscr{S}) = 2 \pi \sum\limits_{k=-K}^{K} \psi_k\left( t ; \mathscr{C}_k \vphantom{0^0}\right)\,\!\delta\!\left(\vphantom{0^0}\omega-{\omega}_k\vphantom{0^0}\right)

can also be visualized.

Example 1

Consider a signal z(t)z(t) which consists of a Dirac delta impulse train with fundamental period TT.

z(t)=∑k=−∞∞δ(t−kT)z(t) = \sum\limits_{k=-\infty}^{\infty}\delta(t-kT)

We can represent this signal with a component set consisting of a set of harmonically related SHCs

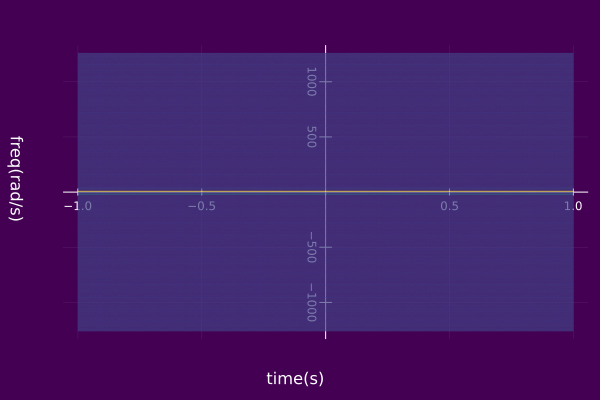
S={⋯ ,C−1,C0,C1,⋯ }, Ck={ak,kω0,ϕk00}, k=0,±1,±2,…\mathscr{S}=\left\{\cdots,\mathscr{C}_{-1},\mathscr{C}_0,\mathscr{C}_1,\cdots\right\},~\mathscr{C}_k = \left\{a_k,k\omega_0, \phi_k\vphantom{0^0}\right\},~k = 0,\pm 1,\pm 2,\ldots

where

ak=abs(1/T)   and   ϕk=arg(1/T).a_k = \mathrm{abs}(1/T)~~~\mathrm{and}~~~\phi_k= \mathrm{arg}(1/T).

For a this choice of parameters of the component set, we have the following Argand Diagram for z(t;S)z(t;\mathscr{S}), 3D IS S(t,ω,s;S)\mathcal{S}(t,\omega,s;\mathscr{S}), and 2D IS S(t,ω;S)\mathcal{S}(t,\omega;\mathscr{S}). Keep in mind, we are only considering a finite number of components k=0,±1,±2,…,Kk = 0,\pm 1,\pm 2,\ldots,K not k=0,±1,±2,…,±∞k = 0,\pm 1,\pm2,\ldots,\pm\infty.

using ISA, Plots
T = 0.5
aₖ(k) = 1/T
kInds = -10:10
𝑆 = fourierSeries(T, aₖ, kInds)
z = AMFMmodel(𝑆)
plot(z; timeaxis=-1.0:0.001:1.0, ylims=(-1.0,1.0))

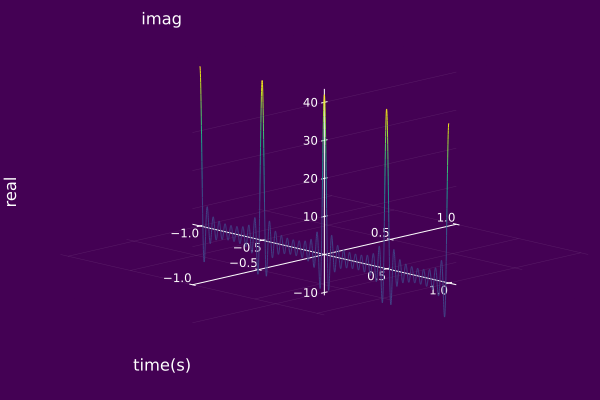
using ISA, Plots
T = 0.5
aₖ(k) = 1/T
kInds = -10:10
𝑆 = fourierSeries(T, aₖ, kInds)
z = AMFMmodel(𝑆)
plot(𝑆, timeaxis=-1.0:0.001:1.0)

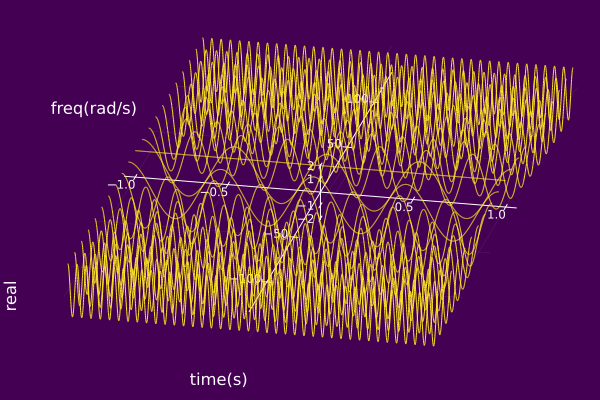
using ISA, Plots
T = 0.5
aₖ(k) = 1/T
kInds = -10:10
𝑆 = fourierSeries(T, aₖ, kInds)
z = AMFMmodel(𝑆)
plot(𝑆, timeaxis=-1.0:0.001:1.0, view="TF",
     left_margin=15Plots.mm, margin=5Plots.mm)

Example 2

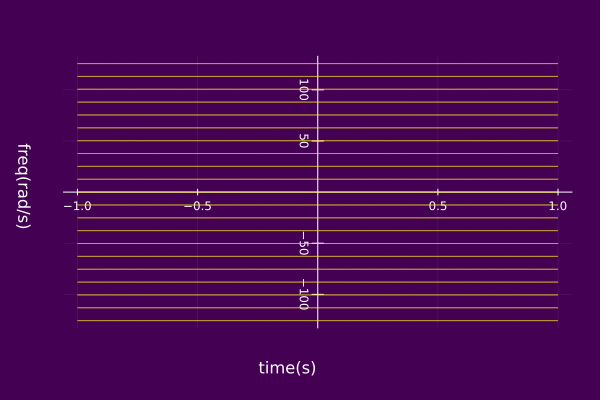
Consider a signal z(t)z(t) which consists of a periodic square wave with a 50% duty cycle where one period TT is defined by

z(t)={1,∣t∣<T/40,T/4<∣t∣<T/2.z(t) = \begin{cases} 1, & |t|<T/4 \\ 0, & T/4<|t|<T/2 \end{cases}.

We can represent this signal with a component set consisting of a set of harmonically related SHCs

S={⋯ ,C−1,C0,C1,⋯ }, Ck={ak,kω0,ϕk00}, k=0,±1,±2,…\mathscr{S}=\left\{\cdots,\mathscr{C}_{-1},\mathscr{C}_0,\mathscr{C}_1,\cdots\right\},~\mathscr{C}_k = \left\{a_k,k\omega_0, \phi_k\vphantom{0^0}\right\},~k = 0,\pm 1,\pm 2,\ldots

where

ak=abs(sin⁡(kπ/2)kπ)   and   ϕk=arg(sin⁡(kπ/2)kπ).a_k = \mathrm{abs}\left(\frac{\sin(k\pi/2)}{k\pi}\right)~~~\mathrm{and}~~~\phi_k= \mathrm{arg}\left(\frac{\sin(k\pi/2)}{k\pi}\right).

For a this choice of parameters of the component set, we have the following Argand Diagram for z(t;S)z(t;\mathscr{S}), 3D IS S(t,ω,s;S)\mathcal{S}(t,\omega,s;\mathscr{S}), and 2D IS S(t,ω;S)\mathcal{S}(t,\omega;\mathscr{S}). Keep in mind, we are only considering a finite number of components k=0,±1,±2,…,Kk = 0,\pm 1,\pm 2,\ldots,K not k=0,±1,±2,…,±∞k = 0,\pm 1,\pm2,\ldots,\pm\infty.

using ISA, Plots
T = 0.5
aₖ(k) = ifelse( k==0, 1/2, sin(k*π/2)/(k*π) )
kInds = -10:10
𝑆 = fourierSeries(T, aₖ, kInds)
z = AMFMmodel(𝑆)
plot(z; timeaxis=-1.0:0.001:1.0, ylims=(-1.0,1.0))

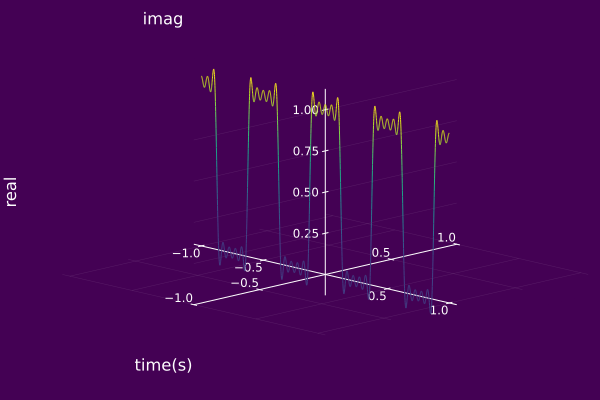
using ISA, Plots
T = 0.5
aₖ(k) = ifelse( k==0, 1/2, sin(k*π/2)/(k*π) )
kInds = -10:10
𝑆 = fourierSeries(T, aₖ, kInds)
z = AMFMmodel(𝑆)
plot(𝑆, timeaxis=-1.0:0.001:1.0)

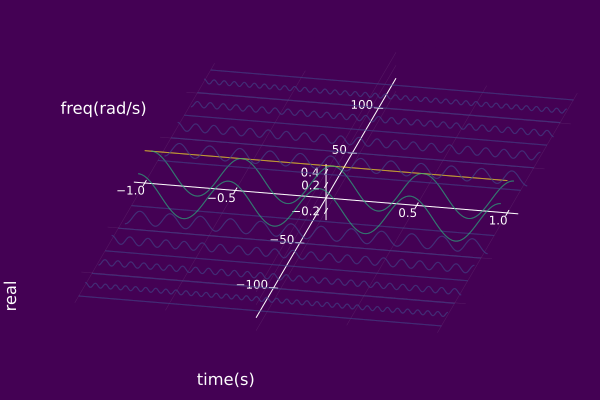
using ISA, Plots
T = 0.5
aₖ(k) = ifelse( k==0, 1/2, sin(k*π/2)/(k*π) )
kInds = -10:10
𝑆 = fourierSeries(T, aₖ, kInds)
z = AMFMmodel(𝑆)
plot(𝑆, timeaxis=-1.0:0.001:1.0, view="TF",
     left_margin=15Plots.mm, margin=5Plots.mm)

Example 3

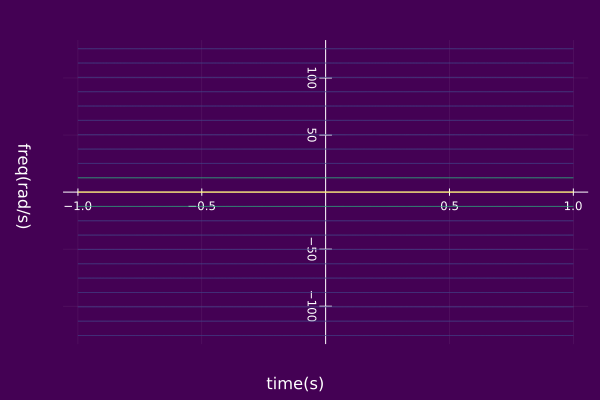
Consider a signal z(t)z(t) which consists of a the periodic square wave (fundamental period TT) with a 50% duty cycle where one period is defined by

z(t)={1,0<t<T/3e j2π/3,T/3<t<2T/3e j4π/3,2T/3<t<T.z(t) = \begin{cases} 1, & 0<t<T/3 \\ \mathrm{e}^{\,\mathrm{j 2\pi/3}} , & T/3<t<2T/3 \\ \mathrm{e}^{\,\mathrm{j} 4\pi/3}, & 2T/3<t<T \end{cases}.

We can represent this signal with component set consisting of a set of harmonically related SHCs

S={⋯ ,C−1,C0,C1,⋯ }, Ck={ak,kω0,ϕk00}, k=0,±1,±2,…\mathscr{S}=\left\{\cdots,\mathscr{C}_{-1},\mathscr{C}_0,\mathscr{C}_1,\cdots\right\},~\mathscr{C}_k = \left\{a_k,k\omega_0, \phi_k\vphantom{0^0}\right\},~k = 0,\pm 1,\pm 2,\ldots

where

ak=abs(1−e−jk2π/3−ej2π/3e−jk4π/3+ej2π/3e−jk2π/3−ej4π3e−jk2π+ej4π/3e−jk4π/3jk2π)   and   ϕk=arg(1−e−jk2π/3−ej2π/3e−jk4π/3+ej2π/3e−jk2π/3−ej4π3e−jk2π+ej4π/3e−jk4π/3jk2π).a_k = \mathrm{abs}\left(\frac{1-\mathrm{e}^{-\mathrm{j}k2π/3}-\mathrm{e}^{\mathrm{j}2π/3}\mathrm{e}^{-\mathrm{j}k4π/3}+\mathrm{e}^{\mathrm{j}2π/3}\mathrm{e}^{-\mathrm{j}k2π/3}-\mathrm{e}^{\mathrm{j}4π3}\mathrm{e}^{-\mathrm{j}k2π}+\mathrm{e}^{\mathrm{j}4π/3}\mathrm{e}^{-\mathrm{j}k4π/3}}{\mathrm{j}k2π}\right)~~~\mathrm{and}~~~\\ \phi_k= \mathrm{arg}\left(\frac{1-\mathrm{e}^{-\mathrm{j}k2π/3}-\mathrm{e}^{\mathrm{j}2π/3}\mathrm{e}^{-\mathrm{j}k4π/3}+\mathrm{e}^{\mathrm{j}2π/3}\mathrm{e}^{-\mathrm{j}k2π/3}-\mathrm{e}^{\mathrm{j}4π3}\mathrm{e}^{-\mathrm{j}k2π}+\mathrm{e}^{\mathrm{j}4π/3}\mathrm{e}^{-\mathrm{j}k4π/3}}{\mathrm{j}k2π}\right).

For a this choice of parameters of the component set, we have the following Argand Diagram for z(t;S)z(t;\mathscr{S}), 3D IS S(t,ω,s;S)\mathcal{S}(t,\omega,s;\mathscr{S}), and 2D IS S(t,ω;S)\mathcal{S}(t,\omega;\mathscr{S}). Keep in mind, we are only considering a finite number of components k=0,±1,±2,…,Kk = 0,\pm 1,\pm 2,\ldots,K not k=0,±1,±2,…,±∞k = 0,\pm 1,\pm2,\ldots,\pm\infty.

using ISA, Plots
T = 0.75
j=im
aₖ(k) = ifelse( k==0, 0, (1-exp(-j*k*2π/3)-exp(j*2π/3)*
exp(-j*k*4π/3)+exp(j*2π/3)*exp(-j*k*2π/3)-exp(j*4π/3)*
exp(-j*k*2π)+exp(j*4π/3)*exp(-j*k*4π/3))/(j*k*2π) )

kInds = -150:150
𝑆 = fourierSeries(T, aₖ, kInds)
z = AMFMmodel(𝑆)
plot(z; timeaxis=-1.0:0.001:1.0, camera=(60,15))

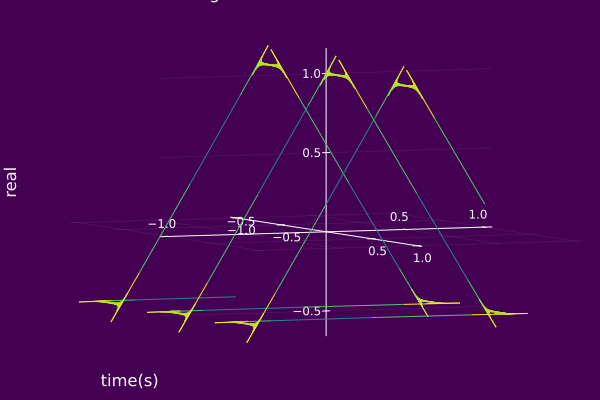
using ISA, Plots
T = 0.75
j=im
aₖ(k) = ifelse( k==0, 0, (1-exp(-j*k*2π/3)-exp(j*2π/3)*
exp(-j*k*4π/3)+exp(j*2π/3)*exp(-j*k*2π/3)-exp(j*4π/3)*
exp(-j*k*2π)+exp(j*4π/3)*exp(-j*k*4π/3))/(j*k*2π) )

kInds = -150:150
𝑆 = fourierSeries(T, aₖ, kInds)
z = AMFMmodel(𝑆)
plot(𝑆, timeaxis=-1.0:0.001:1.0)

using ISA, Plots
T = 0.75
j=im
aₖ(k) = ifelse( k==0, 0, (1-exp(-j*k*2π/3)-exp(j*2π/3)*
exp(-j*k*4π/3)+exp(j*2π/3)*exp(-j*k*2π/3)-exp(j*4π/3)*
exp(-j*k*2π)+exp(j*4π/3)*exp(-j*k*4π/3))/(j*k*2π) )

kInds = -150:150
𝑆 = fourierSeries(T, aₖ, kInds)
z = AMFMmodel(𝑆)
plot(𝑆, timeaxis=-1.0:0.001:1.0)
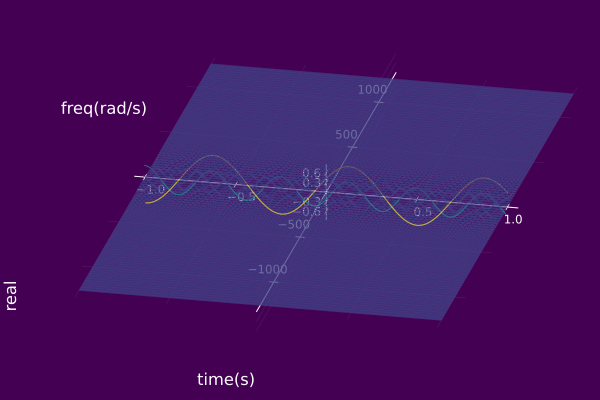
plot(𝑆, timeaxis=-1.0:0.001:1.0, view="TF",
     left_margin=15Plots.mm, margin=5Plots.mm)